Checking statistical properties of protocols using TLA+
In my previous post, I mentioned how excited I was about Jack Vanlightly and Markus Kuppe's talk at TLA+ Conference. They showed a new mode (called "generate") added to the TLA+ checker to enable obtaining statistical properties from the models. Here is how this works in a nutshell. Your TLA+ model/protocol produces a tree of runs, and, in the generate mode the TLA+ checker chooses these runs in a uniform manner. You also specify some state constraints, and when these are satisfied the TLA+ checker executes/evaluates your state constraint formula: you add the statistics logging as the side effect of this formula, and record information about the current run to a CSV file. This way, you can collect statistical hyper properties (abort rates, completion rounds, etc.) about the runs, in addition to checking it for correctness invariants. Later you can use Excel or Rscript to visualize the statistics collected and analyze the model behavior.
Checking statistics is very useful, because ensuring correctness addresses only one part of our concerns with practical systems. Performance, availability, recovery speed are also important dimensions of practical systems. We could of course write a Python simulator and check these properties there, but then we would lose the guarantees that the system is coded correctly (it is easy to introduce bugs while translating the model). Doing these statistical checks in TLA+ allows us to optimize and fine-tune the system all the while preserving its safety-liveness properties via model checking.
This is so cool, and I thought I should learn this, and what better way is there to learn something than trying it hands on using a simple example. I chose Dijkstra's elegant self-stabilizing token ring problem (EWD 426) as the example. Checking statistical properties of this went well and easy. Of course, I botched it and got stuck couple of times: Making mistakes is how we learn. I got help from Markus to get unstuck, so the resulting model is joint work with him. The model is available here under TLA+ examples.
I now have a decent understanding of how this works, and I look forward to applying it to more complex models. The basic scheme is very hackable and it is possible to extend statistics collection for more ambitious efforts. Jack already gave some examples of applying statistics checking to some SWIM, RabbitMQ, and Kafka models.
EWD 426: Stabilizing token ring protocol
EWD 426 is a simple protocol, but it is also a profound one. This simple protocol, "Self-stabilizing systems in spite of distributed control", started the entire field of stabilizing fault-tolerance.
I wrote about this protocol before and even gave a Pluscal model. Here is how the protocol works.
The nodes/processes are arranged in a ring topology. The protocol maintains a unique token circulating this ring. You can think of the token as providing mutual exclusion to the processes; whichever process has the token can access the critical-section/shared-resource.
In the good/invariant states there is exactly one token. So in the faulty states, there are two broad cases: 1) we end up with a ring with no tokens, 2) we end up with a ring with multiple tokens.
Let's consider how Dijkstra's token ring algorithm deals with case 1. Dijkstra's token ring algorithm maps the concept of a physical token to a relation between two neighboring processes. This mapping is done skillfully to limit the state space so the case 1 faults cannot possibly happen in that state space. In the mapped state space, any arbitrary state is guaranteed to contain 1 or more tokens. How does this work? Dijstra's algorithm encodes a token with the relation: "the c variable of a process is DIFFERENT than the c variable of its immediate predecessor in the ring". So, if all c variables are the same, there won't be any token in the system. To prevent this, the algorithm encodes the token differently for process 0: "There is a token at process 0, if its c variable is the SAME as that of its predecessor, process N". Encoded this way, we cannot not have 0 tokens in any arbitrary state in the state space.
In order to deal with case 2, Dijkstra's algorithm uses a token overwriting action to eat some tokens on a best effort fashion. The action is to copy the c value of your predecessor, when your c value is different than its c value (hence, you have the token). In the normal/fault-free case, by taking an action a process consumes a token that exists between its predecessor and itself and passes this token to its successor. In the faulty states case, this is also the worst damage the action can do, because the process will always consume the token at itself, and since its state change affects only its successor, it may or may not pass the token to its successor. If the process execution does not pass the token to its successor, this is actually good: two tokens are removed from the system (one between it and its predecessor, and the other between it and its successor). If enough of these remove token behavior happens, the system will stabilize to exactly one token case.
But what if the remove token behavior leads to a system with no tokens? Recall that this cannot happen due to the discussion regarding Case 1.
Stabilizing token ring model
The Pluscal version is fine, but I wanted to give a clean and simpler TLA+ version. I was inspired by the slick VSCode interface Markus demoed to me earlier in the TLA+ conference to write clean solid engineered code. If written cleanly, TLA+ models are easy to read. (I am channeling the Paxos Made Simple abstract.)
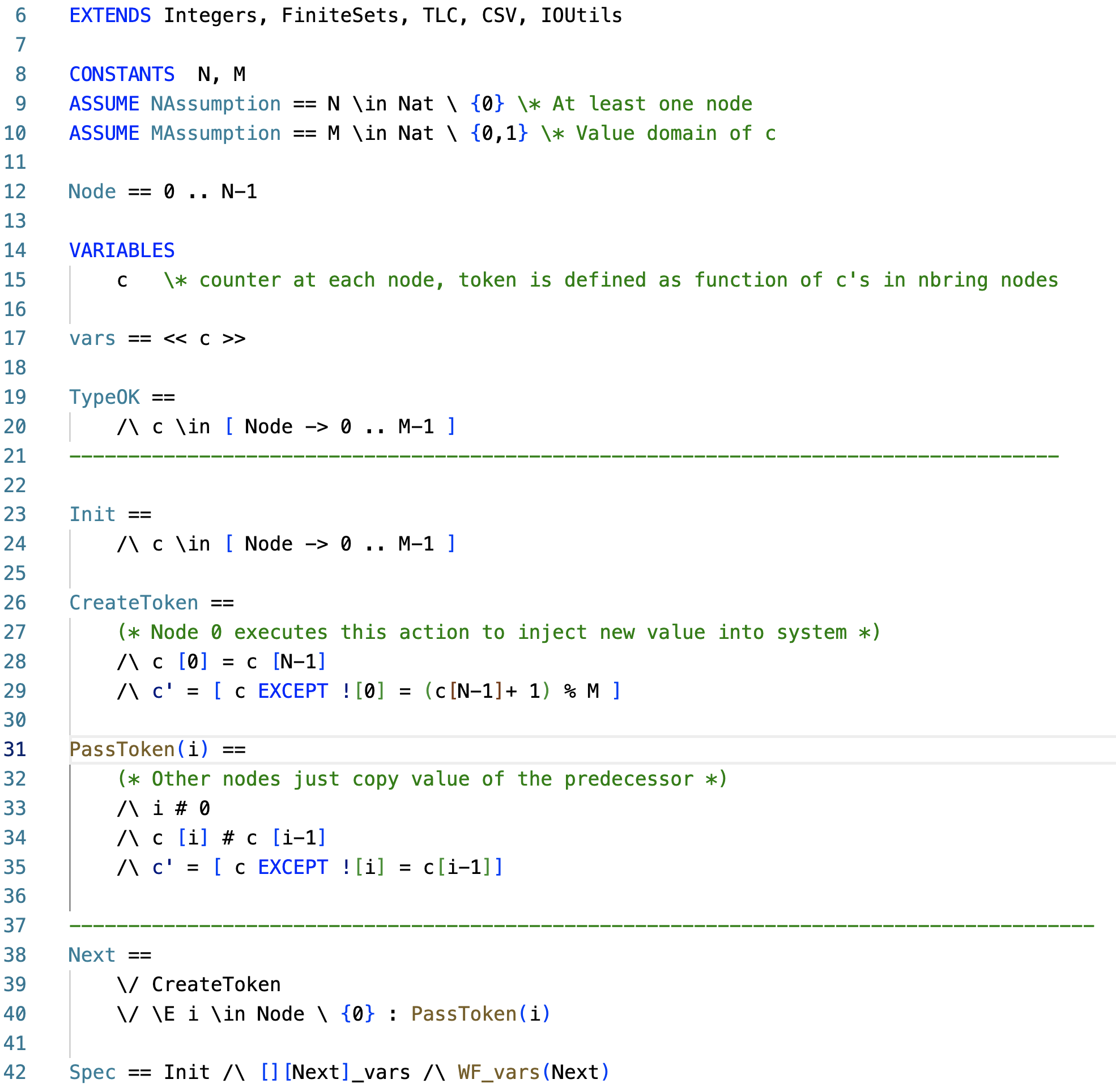
Above is the model. I make the nodes start with arbitrary c values in line 23, since I like to model check stabilization to a unique token. Line 26 is the CreateToken action, which only process 0 executes. It is enabled if c[0] = c[N-1], and it sets c[0] to C[N-1]+1 in modulo M.
Line 31 is the PassToken action executed by processes that are not process 0. This is enabled if the predecessor has a different c value than the node c [i] # c [i-1], and this copies the value of c[i-1] to c[i].
In the invariant states, there is only one token in the system. The two-line UniqueToken predicate captures this property. It says that unique token is true iff there exists a node i such that
- for all nodes from 0 to i, c values are equal to the c value of 0, and
- for all nodes from i to N-1, c values are equal to c[0] -1 in modulo M.
Model checking EWD 426
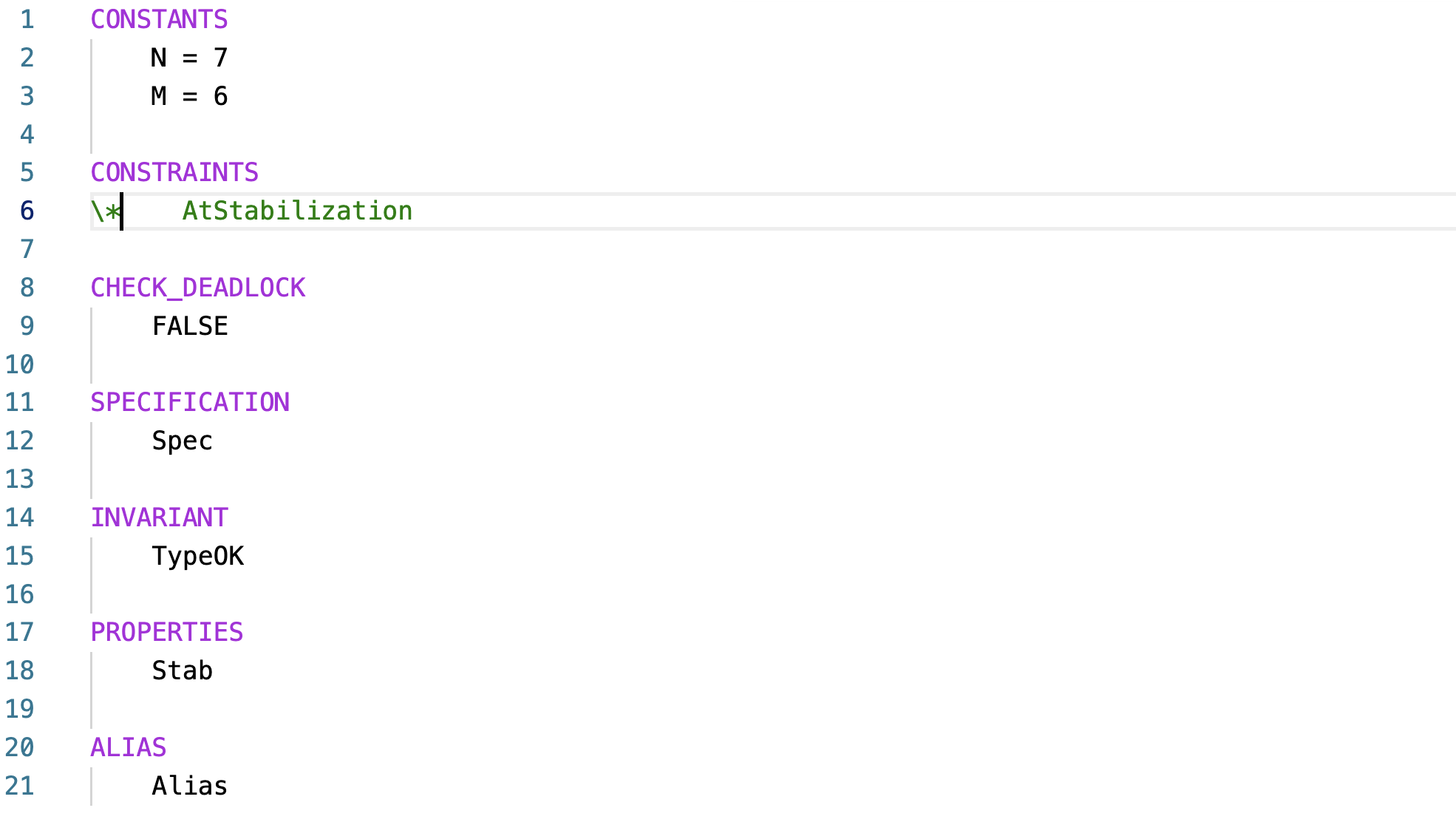
The .cfg file carries the configuration of the model checking. Using the TLA+ toolkit, it was frustrating not to be able to give the model checking instructions well. I would use the comments to say that you can instantiate the model with these constants, and you can use the following properties for model checking. But several things would still be missing, like whether we turn off deadlock checking or not. Now, this cfg file captures all the model checking parameters. This is also version control friendly. If the name of the cfg file is the same as the tla file, it will automatically get picked up by the TLA+ checker. With developers using TLA+ more and more, the TLA+ tools improved significantly to cater to the development best practices.So here is the .cfg for model checking EWD 426. I will change this slightly for statistics collection (there I will un-comment the state constraints line).
Since EWD426 is supposed to show case stabilization, I make the system start in an arbitrary state (see line 23) and check that it stabilizes to invariant states. So I am not checking UniqueToken as the invariant, clearly it would be violated at the start. Instead, I am model checking stabilization to UniqueToken. This is very easy to write. Stab == <>[] UniqueToken
Relation between M and N
If we choose M<N-1, we lose stabilization. Check it yourself to see how this happens. TLA+ will give you a counterexample where a looped-execution is able to keep more than one token in the system forever. In this execution, Node 0 is tricked into creating a new token ad infinitum, when there is already a token somewhere in the inner nodes.At M=N-1 (or above), a phase transition happens. The node 0 is now able to act as a gate. Consider the case where node 0 never fires. In this case the other nodes fire, and eventually they all copy the c value at node 0, and in that configuration the system reduces to one token (at node 0) and stabilization is achieved. For M=N-1 and above, the pigeon-hole principle applies to show that the c value of Node 0 eventually reaches a different value than in the inner nodes, and node 0 does not fire until all other nodes copy its value.
Setting up for checking statistics
Here is the easiest way to set up your laptop for TLA+ statistics checking. Install the TLA+ nightly build VSCode extension. The statistics checking is only available in the nightly build extension.When you are model checking, bring up the command palette by pressing option-X, and select "TLA+ Check Model with TLC" and enter "-coverage 1", so that the checker will report on its model checking progress back to you every minute.
When you are checking statistics, you do the same thing again. Press option-X, and select "TLA+ Check Model with TLC". But this time you will enter a different prompt: "-generate -depth N". The generate mode is recently added: in this mode the TLA+ checker chooses enabled actions in a uniformly random manner and executes sample runs from your model one after the other.
N is an integer. N=-1 this means that the TLA+ checker executes each run until deadlock, and then moves to new run. N=50 means that the TLA+ checker will execute each run upto 50 steps deep, then move to a new run.
Now, I uncomment the state constraints line in the cfg file, and we are ready to check statistics for EWD 426.
Mechanics of statistics collection
The core of idea in logging/collecting statistics is to State/Action constraints as a hook to record statistics from each run to a CSV file. Recording every action in a run would not be useful. You want to record when something significant occurs. TLA+ let's you write state predicates and action properties to capture any interesting stuff you can think of.Originally, the TLA+ checker used these constraints to stop exploring a run when the execution is not desirable anymore. Now we hijack the same mechanism, and use the side effects of the state/action constraints to perform statistics collection. Here is the state constraint I added to collect statistics.
This is a hook that is run for each state encountered. The left hand side of the implication evaluates the UniqueToken predicate on the current global state the TLA+ checker encountered in this particular run. If UniqueToken does not hold, the left hand side becomes FALSE, and makes the implication statement TRUE, so the state constraint returns TRUE. The right-hand side is not even evaluated because the left-hand-side is FALSE. Returning TRUE means the run will continue to the next state. The TLA+ checker chooses another enabled action uniformly random and evaluates the StateConstraint on the new state found.
When UniqueToken holds for a state, the right-hand side of the implication is taken. Here we use TLCGet to get "level", which indicates the current depth of steps in to this particular run, when UniqueToken is truthified. CSVWrite adds this line of statistics into the CSVFile we denoted earlier. For this to work, we imported CSV in the EXTENDS line.
When UniqueToken holds, we like to stop exploring so we add conjunction FALSE to the right hand side, making the expression return FALSE (after having done the CSVWrite side effect). FALSE tells the checker to stop exploring this particular run, because we got to where we wanted. (I had previously model-checked and ensured that the system always stabilizes, I am not interested in exploring this run to check UniqueToken keeps holding.)
That is how statistics collection works. We invoke this generate mode writing "-generate -depth -1" and let it rip through sampling the runs and collecting statistics. When we stop the TLA checker after a minute, we will have tens of thousands of runs, and hence that many entries in our CSV file. The rest is up to us to process/visualize this data. Use excel if you like. But a more programmatic way of doing this is to use Rscript and write visualizations to an image file, like svg.
We can do this visualization offline, or using a clever hack Markus devised online, while TLA+ checker is running and exploring the runs. Just append this to AtStabilization state constraint. TLCGet("stats") provides information like how many of each action is executed in a run, how many runs has been explored, etc. This line invokes Rscript on the CSV file after every 250 runs explored. Each time it is invoked, Rscript regenerates the svg image, and using the svg viewer in VSCode, we see the statistics changing in real time.
There is also TLCSet command, which can give you more flexibility in logging/collecting statistics. TLCSet can be used to store things to a register, registers are numbered starting from 1. Later you can TLCGet that register to read what you memorized earlier in this particular run, or even in previous runs. Markus showed an example of this in his Termination Detection model.
Analysis
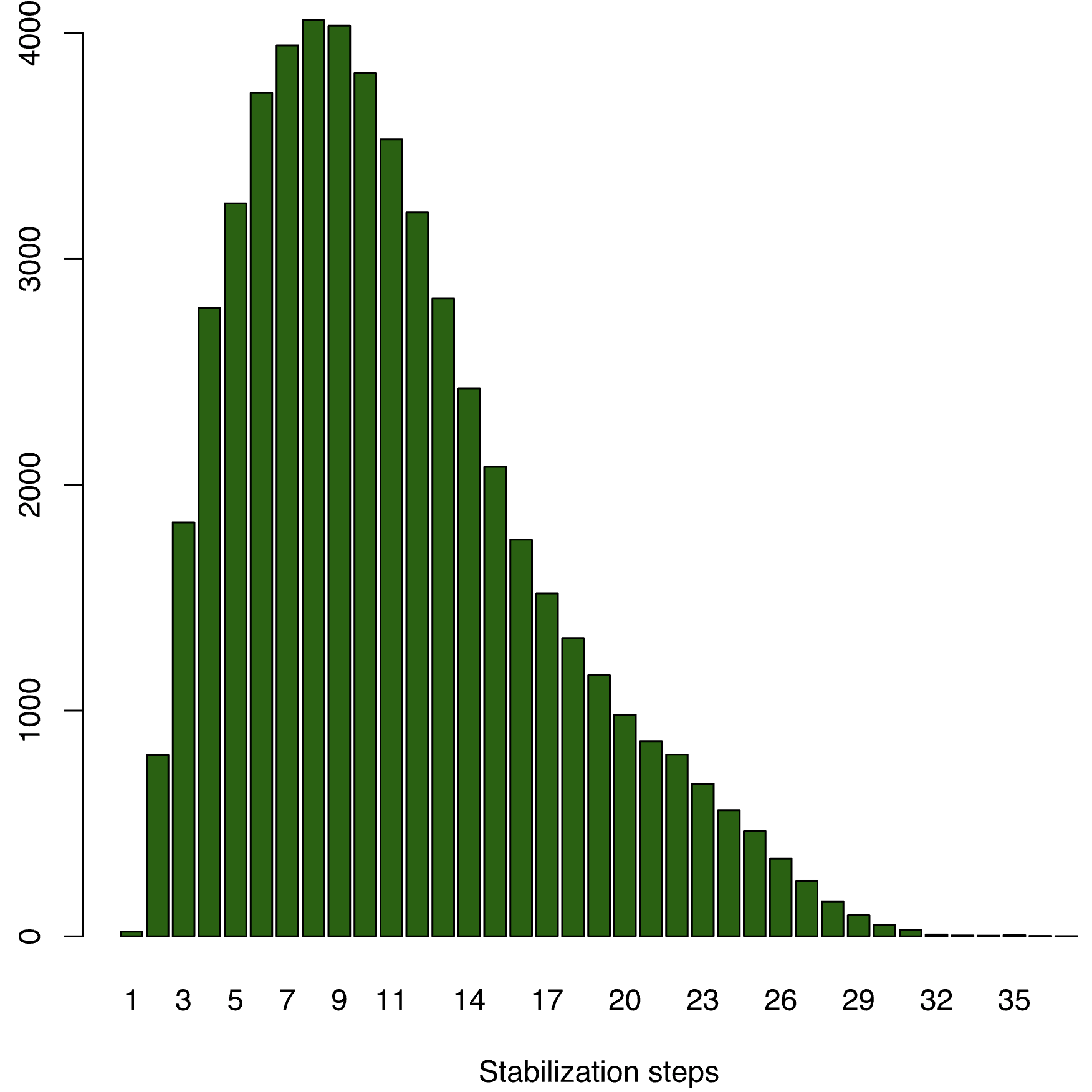
Let's check the statistics we collected. Here is the histogram for N=7 and M=6 configuration. There is a nice uniform distribution of number of steps required for stabilization. 10 steps seem to be the average. There is a bump at step 1, but this is due to some initial states being those for which UniqueToken already holds.But for M=3, this works, because probabilistically it is hard to hit the looping run here. This makes the average stabilization at 8-9 steps and skews the distribution toward the left, and somehow makes the tail more pronounced. That is not much of an improvement. Although we capped the M domain, the N domain still throws us significant number of state configurations. Since there are many nodes whose states need to be fixed and aligned globally.
The theoretical worst case for stabilization of EWD 426 is M*N. For N=7 and M=6 that makes 42, but we see that in practice stabilization occurs much earlier. And for N=7 and M=3 (an unsafe configuration), we don't see significant improvement in stabilization time over the safe configuration.
Debugging via TLA+
Of course I didn't get the TLA+ model work in one shot. I had made boundary condition errors in definition of UniqueToken. The VSCode TLA+ checker now includes debugging support and that helped me. Markus shared a video about this recently. Markus added this support in a generalizable way through Debug Adapter Protocol (DAP), so the community can extend the debugging support to Intellij and CLI.What blew my mind in the debuggin mode was that if you add a breakpoint in the Spec line and run TLC in Debug mode using -simulate prompt, you can use the VSCode debug menu to skip over an action or step into that action, backtrack and move forward again. This way you can control how the run goes, navigate it to particular tricky situations and see what goes there.
Another cool trick is to add an ALIAS in the cfg file, to improve how debugging information is presented to you. Instead of raw state debuggging, you can make the definitions work for you and provide you the predicates you care about the raw state. Here is the alias predicate I used to get a high level view of the state.








Comments