Oblivious Paxos: Privacy-Preserving Consensus Over Secret-Shares

This paper appeared in SOCC'23. The paper presents a primary-backup secret-shared state machine (PBSSM) architecture and the associated consensus protocol, Oblivious Paxos (OPaxos). OPaxos enables privacy-preserving consensus by allowing acceptors to safely and consistently agree on a secret-shared value without untrusted acceptors knowing the value.

OPaxos protocol overview

OPaxos uses (t, n) threshold secret-sharing. This means generating n secret-shares from a single secret value such that it is possible to reconstruct the secret with just t shares.

In order to make (t, n) threshold secret-sharing play well with Paxos, the protocol requires that the cardinality of the intersection of any phase1 quorum and phase2 quorum is larger than t. 

This can be achieved by choosing the quorum size as (n+t)/2. More accurately,  one quorum (say phase1) would have cardinality as the ceiling of (n+t)/2, and the other quorum (phase2) would have cardinality as floor of this (n+t)/2. The justification is quite simple. If we sum the cardinality of the two quorums, we get n+t, but there are only n pigeon-holes (erm, total nodes), so we know that these two quorums intersect at least at t nodes.

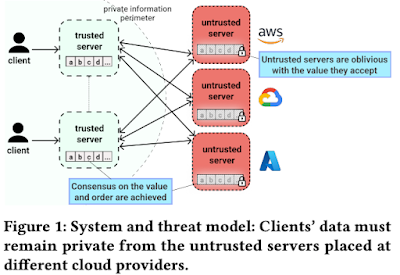
In the setup below n=5 and t=2. That means p1=4 nodes, and p2=3 nodes. Note that leaders are only allowed to be located in the trusted sites, and an acceptor in an untrusted site is not allowed to be a leader.

In the appendix, the paper shows how the (t,n) idea can be extended to Fast Paxos. Since the idea is simple and applies at the quorum intersection level, I think the idea also applies for other flavors, even for Nezha, which we reviewed recently.

What problem is the paper solving?

Integrating the (t,n) threshold secret-sharing to Paxos is cute, but the motivation is not well justified. The paper gives hybrid cloud deployments as an application, where the cloud sites are designated as untrusted and leaders are run only at the trusted sites. 

If the leader on the trusted site uses encryption for the content of the messages, and uses acceptors at the untrusted sites to accept and replicate encrypted content, we would achieve the same objective using vanilla Paxos. The untrusted sites would still be oblivious to the content of the messages they accept and logs they replicate, since they don't have the encryption keys.

The paper mentions that encryption does not offer information-theoretic privacy because a computationally rich adversary may break it eventually. This is not a practical concern. This is in fact much more unlikely than the cloud providers used in (t,n) secret sharing colluding with each other to reveal the secret.

The paper does not justify the need for coupling secrecy with Paxos-consensus, when it is easy to achieve both benefits in a decoupled manner. Decoupled components is better for managing complexity and keeping flexible options for software/system evolution.

Note that, in OPaxos, none of those acceptors in the untrusted sites are allowed to become a leader anyways, because if they do they would have access to information from other nodes and can decrypt the secrets as they would obtain more than t shares. Actually, this opens an interesting attack vector for OPaxos. What stops them from becoming leaders?

So what is the benefit we gain from the untrusted sites, if availability of the system is limited to availability of at least one node in the trusted sites? The paper suggests that, if the nodes at the trusted sites become unavailable, the untrusted nodes can fall back to using secure multi-party computation (SMPC) to preserve availability of the system while keeping secrecy. There are no details in the paper (except for a paragraph) as to how this can be achieved. SMPC is an involved topic and is currently not available for general computation required for state machine replication. So I don't think we can count this as an argument in favor of using OPaxos and (t,n) secret sharing. 

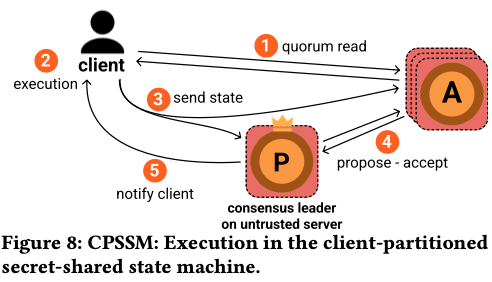
But, as a rebound, the paper does mention an advantage to using OPaxos and (t,n) sharing if we consider the simple stateless problem of key-value store maintenance with just GET and PUT. Then thanks to (t,n) secret sharing, even when no trusted site is available, the client can reach out to the untrusted nodes, and get service in a secrecy preserving manner as follows: "To execute a request, a client dealer fetches the state partition it manages, e.g., a key-value pair, locally computes the result and re-distributes secret shares of any state modifications back to the untrusted servers (shown in Figure 8). It is straightforward to ensure request privacy by performing both read and write operations in a manner so as to appear identical, e.g., by always updating a nonce in the key-value pair even for reads to make them indistinguishable from writes."

The paper has Go implementation for this untrusted execution mode of key-value store maintenance in its Github repo.  (And of course, no implementation for the SMPC mode.) For implementation of OPaxos and Fast-OPaxos, the paper builds on our (Ailidani Ailijiang, Aleksey Charapko, and Murat Demirbas) Paxi framework implementation.

SMR maintenance in OPaxos

I want to mention another interesting tidbit about the paper. OPaxos shares the state-diff resulting from speculative operation execution at one of the leaders at the trusted sites. The paper argues that this avoids the need to have deterministic op-logs, but they miss the importance of change data capture (CDC). Oplogs are essential for the CDC-based data/system integration in the cloud ecosystem via capturing and delivering changes made.

I think OPaxos would still be amenable to using oplogs, by having learners at trusted domains running as hot-swap-host catching up and executing from oplogs.