Open Versus Closed: A Cautionary Tale

This paper appeared in NSDI'06. It explores the behavior of open and closed system models. These two models differ in how they handle new job arrivals. In an open system model, new jobs arrive independently of job completions. In contrast, in a closed system model, new jobs are only triggered by job completions, followed by think time.

The paper makes a basic but an important point that was missed by many people that were building workload generators and making system design decisions. In this sense this is a great demonstration of the thesis that "The function of academic writing is NOT to communicate your ideas, but to change the ideas of an existing community."

The paper shows that while most workload generators model systems as closed systems, in reality the systems are closer to open systems, and conclusions drawn from closed model behavior of the systems do not translate to the performance of the systems in real-world settings.   

Here is the gist of the idea. For a given load, mean response times are significantly lower in closed systems than in open systems. In other words, closed system modeling/evaluation is unrealistically protected from overloading effects that happen in the real world, even when compared to the open system modeling/evaluation with the same load. Suppose the system has an average arrival rate of 10 requests per second, and the system is able to keep up with 10 requests per second. In an open system (which is more close to reality) it is possible that by random chance this limit will be exceeded. (Theoretically,  the number of users queued or running at the system at any time may range from zero to infinity.) When this happens some requests will remain unanswered/pending, and will delay other requests and cause a downward spiral. When you evaluate your system under closed system model/evaluation, you don't catch this problem, and you get overconfident about the system, only to be frustrated in real deployment by unavailability and failures. The load a closed model generates is too protective and is misleading: Your system may not be able to handle the same average load in real world when the behavior is closer to an open model. Or at least you will see high tail latencies you did not anticipate.

The paper makes this point comprehensively by surveying existing workload generators, and using a combination of implementation and simulation experiments on systems including web servers serving static HTTP requests in both a LAN/WAN setting; the back-end database in an e-commerce applications, and an auctioning web site. It identifies eight guiding principles that identifies how scheduling policies are impacted by closed and open models and explain the differences in user level performance. These principles also provide guidelines for system designers to determine which model is most appropriate for a given workload. Additionally, the paper proposes that partly open system models may offer the best compromise between open and closed models.

Read on for a more detailed summary of the paper.

Sidebar: Performance Modeling book!

Mor Harchol-Balter, an author of this paper, is the author of the 2013 book "Performance Modeling and Design of Computer Systems: Queueing Theory in Action". This book provides a great and relatively approachable coverage of performance modeling and some queueing theory. Jesse Jiryu Davis, Andrew Helwer, and I have been going through this book by meeting one hour every other week. This was an enjoyable experience. I really liked the Socratic question/answering method used in the book. I also got transported back to my High School experience, where using basic algebra we attacked problems in physics and chemistry in a high ROI manner. The book made me see again that basic math can take you a long way. The notation and terminology could be more accessible, but it is understandable that the book had to go with the classic queueing theory notations and terminologies... It is a textbook after all. I think there is room for writing a more accessible version of the book targeting system designers, with hands-on Python examples.  

Here is a short tutorial presentation by Mor, which I hope will convince you to study her book. To reiterate, these concepts are basic but powerful.

Setup

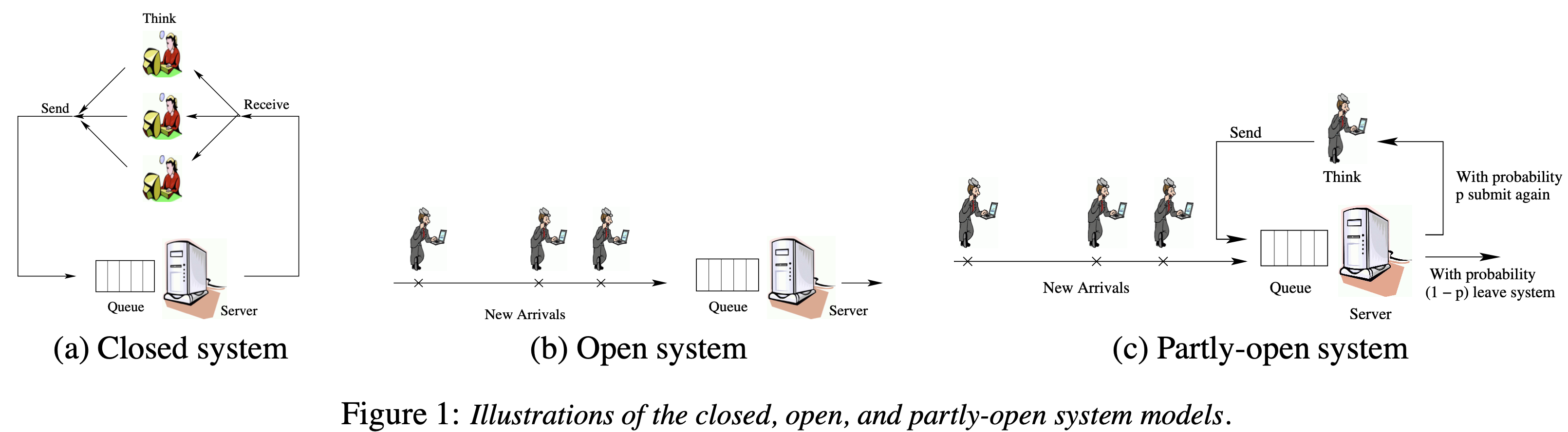
In a closed system as shown in Fig 1.a, the number of users is typically called the multiprogramming level (MPL) and denoted by N. Each of these N users repeats these 2 steps, indefinitely: (a) submit a job, (b) receive the response and then “think” for some amount of time. In a closed system, a new request is only triggered by the completion of a previous request. At all times there are some number of users, N-think, who are thinking, and some number of users N-system, who are either running or queued to run in the system, where N-think + N-system = N . The response time, T , in a closed system is defined to be the time from when a re- quest is submitted until it is received. In the case where the system is a single server (e.g. a web server), the server load, denoted by ρ, is defined as the fraction of time that the server is busy, and is the product of the mean throughput X and the mean service demand (processing requirement) E[S].

In an open system model there is a stream of arriving users with average arrival rate λ. Each user is assumed to submit one job to the system, wait to receive the response, and then leave. The number of users queued or running at the system at any time may range from zero to infinity. The differentiating feature of an open system is that a request completion does not trigger a new request: a new request is only triggered by a new user arrival. As before, response time, T , is defined as the time from when a request is submitted until it is completed. The server load is defined as the fraction of time that the server is busy. Here load, ρ, is the product of the mean arrival rate of requests, λ, and the mean service demand E[S].

In order to fairly compare the open and closed systems, the experiments hold the system load ρ for the two systems equal, and study the effect of open versus closed system models on mean response time.

The scheduling policies considered in the experiments are:

• FCFS (First-Come-First-Served) Jobs are processed in the same order as they arrive.
• PS (Processor-Sharing) The server is shared evenly among all jobs in the system.
• PESJF (Preemptive-Expected-Shortest-Job-First) The job with the smallest expected duration (size) is given preemptive priority.
• SRPT (Shortest-Remaining-Processing-Time-First): At every moment the request with the smallest remain ing processing requirement is given priority.
• PELJF (Preemptive-Expected-Longest-Job-First) The job with the longest expected size is given preemptive priority. PELJF is an example of a policy that performs badly and is included to understand the full range of possible response times.

Real-world case studies and principles derived

The first set of principles describe the difference in mean response time under open and closed system models and how various parameters affect these differences. These are very apparent comparing the first and second columns in Figure 2.

• Principle 1: For a given load, mean response times are significantly lower in closed systems than in open systems. This is because the closed system has a fixed number of users that limits the queue length, while the open system has no such limit.
• Principle 2: As the multiprogramming level (MPL) grows, closed systems become open, but convergence is slow for practical purposes. This is because the closed system still behaves “closed” with respect to mean response time even for high MPLs, especially when the service demands are highly variable.
• Principle 3: While variability has a large effect in open systems, the effect is much smaller in closed systems. This is because the variability in service demands affects both the queueing time and the service time in open systems, but only the service time in closed systems.

The second set of principles deal with the impact of scheduling on improving system performance. Scheduling is a common mechanism for improving mean response time without purchasing additional resources. By just checking Figure 2, it is also apparent that the impact of scheduling is very different under open and closed models. Favoring short jobs is highly effective in improving mean response time in open systems, while this is far less true under a closed system model. This is because favoring short jobs reduces both the queueing time and the service time in open systems, but only the service time in closed systems.

• Principle 4: While open systems benefit significantly from scheduling with respect to response time, closed systems improve much less.
• Principle 5: Scheduling only significantly improves response time in closed systems under very specific parameter settings: moderate load (think times) and high MPL.
• Principle 6: Scheduling can limit the effect of variability in both open and closed systems.

The third set of principles deal with partly-open systems. While workload generators and benchmarks typically assume either an open system model or a closed system model, many applications are best represented using an “in-between” system model, called the partly-open model. Under the partly-open model, every time a user completes a request at the system, with probability p the user stays and makes a followup request (possibly after some think time), and with probability 1 − p the user simply leaves the system. The expected number of requests that a user makes to the system in a visit is Geometrically distributed with mean 1/(1 − p). The collection of requests a user makes during a visit to the system denotes a session and the length of a session is the number of requests in the session/visit. These principles specify parameter settings for which the partly-open model behaves more like a closed model or more like an open model with respect to response time.

• Principle 7: A partly-open system behaves similarly to an open system when the expected number of requests per session is small (≤ 5 as a rule-of-thumb) and similarly to a closed system when the expected number of requests per session is large (≥ 10 as a rule-of-thumb).
• Principle 8: In a partly-open system, think time has little effect on mean response time. Changing the think time in the partly-open system has no effect on the load because the same amount of work must be processed