SOSP19. I4: Incremental Inference of Inductive Invariants for Verification of Distributed Protocols
This paper is by Haojun Ma (University of Michigan), Aman Goel (University of Michigan), Jean-Baptiste Jeannin (University of Michigan), Manos Kapritsos (University of Michigan), Baris Kasikci (University of Michigan), Karem A. Sakallah (University of Michigan).
This paper is about formal verification of distributed systems. Writing proofs manually is cumbersome. Existing tools for formal verification all require the human to find the inductive invariant.
I4 combines power of Ivy (a tool for interactive verification of infinite-state systems) and model checking in order to find inductive invariant without relying on human intuition. Ivy takes as input a protocol description and a safety property, and guides the user interactively to discover an inductive invariant. The goal for finding an inductive invariant is to prove that the safety property always holds. An inductive proof has a base case, which proves initial state is safe, and an inductive step, which proves if state k is safe, prove state k+1 is safe. Once that inductive invariant is found, Ivy automatically verifies that it is indeed inductive.
The insight in I4 is that the safety/correctness behavior of a distributed system does not fundamentally change as the size increases. I witness this regularly in my use of TLA+ for model checking protocols. TLA+ is able to identify any problem (sometimes requiring upto 40 steps) by finding a counterexample involving three nodes. Three nodes is often what it takes. One node initializes a coordination operation, and the other two nodes see a different perspective of the ongoing computation, maybe due to exchanging messages with each other (i.e. doing stale reads) at inopportune times, and arrive to conflicting decisions that violate the goal of the coordination operation.
I4 uses inductive invariants from small instances and apply/generalize to large instances, and automates this with model-checking. More specifically, I4 first creates a finite instance of the protocol; use a model checking tool to automatically derive the inductive invariant for this finite instance; and generalize this invariant to an inductive invariant for the infinite protocol. This amends the I4 approach in that it automates the inductive invariant discovery process. This amends the model checking approach as well. While model checking is fully automated, it doesn’t scale to distributed systems. I4 applies model checking to small, finite instances and then generalizes the result to all instances.
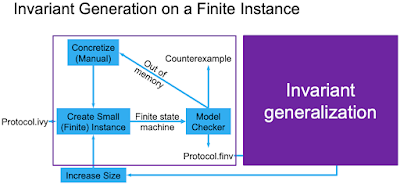
The figure above shows an overview of the I4 flow for the invariant generation on a finite instance.
Safety property P may be an invariant but not an inductive one. "The verification proof requires the derivation of additional invariants that are used to constrain P until it becomes inductive. These additional invariants are viewed as strengthening assertions that remove those parts of P that are not closed under the system's transition relation." In other words, while the safety property holds for reachable states, it may not be closed under program actions outside the reachable states. This makes safety invariant unsuitable for verification since proving properties is not constrained to the reachable states (as it is hard to enumerate/identify reachable states in a proof). So, the inductive invariant is a version of the safety property that is closed under the program actions. The figure below illustrates this relationship. I think this concept is explored further in the Ivy paper.

If the safety property holds, then Averroes generates an inductive invariant for the finite instance; minimizes the invariant by removing redundant clauses; and then passes it on to the next step to be generalized. However, occasionally the finite instance may still be too large for the Averroes model checker, and it may run out of memory. This is where human involvement is needed again. The human helps concretize the small finite version of the protocol further to avoid state space explosion. Symmetry plays a big role here. FIRST is the keyword that denotes the node that sends the first message. The model checker can try instances where all the three nodes in the finite instances might be the one that sends the message. The human can notice a symmetry and set "FIRST = Node1" to help reduce the state space. (The team is working on automating this step as well.)
Then I4 uses Ivy for the proof generation as shown below, and the verification is complete.

I4 is available as opensource at https://github.com/GLaDOS-Michigan/I4. They applied I4 to several examples as shown in the table.

I4 improves on manual verification via using Coq and interactive verification using Ivy.

A restriction in I4 is that it applies to verification of safety properties, and not to liveness properties.
I am happy to find so many verification papers at SOSP. This paper appeared in the distributed systems in the afternoon of Day 2. In the morning of Day 2, there was a session on verification which included four papers. I had reviewed two of these papers earlier: "Scaling Symbolic Evaluation for Automated Verification of Systems Code with Serval" and "Verifying Concurrent, Crash-safe Systems with Perennial". It looks like the verification community at SOSP is quick to take results from more general and theoretic verification conferences, and integrate those tools and improve upon them to put them in use for verification of practical systems.
This paper is about formal verification of distributed systems. Writing proofs manually is cumbersome. Existing tools for formal verification all require the human to find the inductive invariant.
I4 combines power of Ivy (a tool for interactive verification of infinite-state systems) and model checking in order to find inductive invariant without relying on human intuition. Ivy takes as input a protocol description and a safety property, and guides the user interactively to discover an inductive invariant. The goal for finding an inductive invariant is to prove that the safety property always holds. An inductive proof has a base case, which proves initial state is safe, and an inductive step, which proves if state k is safe, prove state k+1 is safe. Once that inductive invariant is found, Ivy automatically verifies that it is indeed inductive.
The insight in I4 is that the safety/correctness behavior of a distributed system does not fundamentally change as the size increases. I witness this regularly in my use of TLA+ for model checking protocols. TLA+ is able to identify any problem (sometimes requiring upto 40 steps) by finding a counterexample involving three nodes. Three nodes is often what it takes. One node initializes a coordination operation, and the other two nodes see a different perspective of the ongoing computation, maybe due to exchanging messages with each other (i.e. doing stale reads) at inopportune times, and arrive to conflicting decisions that violate the goal of the coordination operation.
I4 uses inductive invariants from small instances and apply/generalize to large instances, and automates this with model-checking. More specifically, I4 first creates a finite instance of the protocol; use a model checking tool to automatically derive the inductive invariant for this finite instance; and generalize this invariant to an inductive invariant for the infinite protocol. This amends the I4 approach in that it automates the inductive invariant discovery process. This amends the model checking approach as well. While model checking is fully automated, it doesn’t scale to distributed systems. I4 applies model checking to small, finite instances and then generalizes the result to all instances.

The figure above shows an overview of the I4 flow for the invariant generation on a finite instance.
Given a protocol description--written in Ivy--and an initial size, I4 first generates a finite instance of that protocol with a given initial size. For example, ... I4 will generate a finite instance of the protocol with one server and two clients. It then uses the Averroes model checker to either generate an inductive invariant that proves the correctness of the protocol for that particular instance, or produce a counterexample demonstrating how the protocol can be violated and which can be used to debug the protocol. If the protocol is too complex, the model checker may fail to produce an answer within a reasonable amount of time or it may run out of memory. If this occurs, the finite encoding is simplified—using a concretization technique—to further constrain it and make it easier for the model checker to run to completion. This step is currently done manually but is easily automatable. Once an inductive invariant has been identified, I4 generalizes it to apply not only to the finite instance that produced it, but also to all instances of the protocol.It is important to note that if the safety invariant does not hold, Averroes produces a counterexample and the human should work on the protocol to come up with a safety invariant that holds for the protocol. I4 is automatic, in that if the protocol safety invariant holds, then the inductive invariant is generated automatically by the Averroes tool. But, wait, what is the difference between safety invariant and inductive invariant? Isn't safety invariant already inductive?
Safety property P may be an invariant but not an inductive one. "The verification proof requires the derivation of additional invariants that are used to constrain P until it becomes inductive. These additional invariants are viewed as strengthening assertions that remove those parts of P that are not closed under the system's transition relation." In other words, while the safety property holds for reachable states, it may not be closed under program actions outside the reachable states. This makes safety invariant unsuitable for verification since proving properties is not constrained to the reachable states (as it is hard to enumerate/identify reachable states in a proof). So, the inductive invariant is a version of the safety property that is closed under the program actions. The figure below illustrates this relationship. I think this concept is explored further in the Ivy paper.

If the safety property holds, then Averroes generates an inductive invariant for the finite instance; minimizes the invariant by removing redundant clauses; and then passes it on to the next step to be generalized. However, occasionally the finite instance may still be too large for the Averroes model checker, and it may run out of memory. This is where human involvement is needed again. The human helps concretize the small finite version of the protocol further to avoid state space explosion. Symmetry plays a big role here. FIRST is the keyword that denotes the node that sends the first message. The model checker can try instances where all the three nodes in the finite instances might be the one that sends the message. The human can notice a symmetry and set "FIRST = Node1" to help reduce the state space. (The team is working on automating this step as well.)
Then I4 uses Ivy for the proof generation as shown below, and the verification is complete.

I4 is available as opensource at https://github.com/GLaDOS-Michigan/I4. They applied I4 to several examples as shown in the table.

I4 improves on manual verification via using Coq and interactive verification using Ivy.

A restriction in I4 is that it applies to verification of safety properties, and not to liveness properties.
I am happy to find so many verification papers at SOSP. This paper appeared in the distributed systems in the afternoon of Day 2. In the morning of Day 2, there was a session on verification which included four papers. I had reviewed two of these papers earlier: "Scaling Symbolic Evaluation for Automated Verification of Systems Code with Serval" and "Verifying Concurrent, Crash-safe Systems with Perennial". It looks like the verification community at SOSP is quick to take results from more general and theoretic verification conferences, and integrate those tools and improve upon them to put them in use for verification of practical systems.



Comments