Practical Byzantine Fault Tolerance
This paper is authored by Miguel Castro and Barbara Liskov, and it appeared in OSDI 1999. The conference version has around 2500 citations, and the journal version has close to 1500 citations. This paper is the grandfather for most Byzantine Fault Tolerant (BFT) protocols, including work that appeared through 2000s-2010s at OSDI/SOSP, and more recent blockchain BFT work such as LibraBFT.
Use of techniques like N-version programming may help alleviate the issue. The idea is to implement the same API/specifications in multiple different ways, so that a software error does not constitute a problem for more than one third of the replicas. But this is not easy, also not always effective. Many developers are prone to make similar mistakes/bugs in similar tricky places.
While there has been a decade of followup work to PBFT, since the above problems remained unaddressed, there was also a growing criticism of BFT work. I swear I have seen a couple talks toward 2010 that declared BFT impractical. They had titles like "Do we need BFT" and "BFT is impractical". Unfortunately I cannot find those talks now.
In the last five years or so, with the prominence of blockchains and adversarial commerce applications, BFT assumption/model became relevant again. Therefore, yes, the prediction in the opening of the paper turned out to be appropriate after all.
PBFT is based on replicated state machine (RSM) approach. This is very similar to how Paxos uses RSM to achieve consensus to the face of crash faults. Here, due to Byzantine fault-tolerance, the protocol gets a bit more involved. Also instead of N=2F+1 in Paxos, BFT requires N=3F+1, where F is the upper bound on the number of faulty replicas, and N is the number of replicas in total. The reason is as follows. We cannot wait reply from more than N-F replicas, because the F faulty replicas may not reply. But what if the among the N-F replicas that respond, F of them are faulty replicas? So there must still be enough responses that those from non-faulty replicas outnumber those from faulty ones, i.e., N-2F>F.
The RSM maintenance works pretty similar to Paxos, or rather, viewstamped replication flavor of consensus. The replicas move through a succession of configurations called views (this corresponds to the ballotnumber concept in Paxos). In a view one replica is the primary and the others are followers.
Views are numbered consecutively. The primary of a view is replica p such that p= v mod N. View changes are carried out when it appears that the primary has failed.
The state of each replica includes the state of the service, a message log containing messages the replica has accepted, and an integer v denoting the replica's current view.
PBFT normal operation goes as follows:
1. A client sends a request to invoke a service operation to the primary
2. The primary multicasts the request to the backups
3. Replicas execute the request and send a reply to the client
4. The client waits for F+1 replies from different replicas with the same result; this is the result of the operation
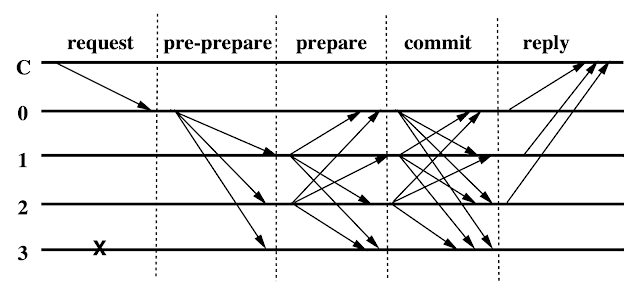
Here the primary is replica 0. There are three phases to commit the request. The pre-prepare and prepare phases are used to totally order requests sent in the same view even when the primary, which proposes the ordering of requests, is faulty. The prepare and commit phases are used to ensure that requests that commit are totally ordered across views.
A backup accepts a pre-prepare message provided:
A replica (including the primary) accepts prepare messages and adds them to its log provided their signatures are correct, their view number equals the replica’s current view, and their sequence number is between h and H.
The predicate, Prepared (m,v,n,i) holds iff replica i has inserted in its log:
The predicated Committed (m,v,n) holds iff Prepared (m,v,n,i) is true for all i in some set of F+1 replicas. And the predicate Committed-local (m,v,n,i) holds iff Prepared (m,v,n,i) is true and i has accepted 2F+1 commits (possibly including its own) matching m.
As an invariant of PBFT, we have that if Committed-local (m,v,n,i) holds, then Committed (m,v,n) holds. This ensures that non-faulty replicas agree on the sequence numbers of requests that commit locally even if they commit in different views at each replica. Furthermore, with the view change protocol this ensures that any request that commits locally at a non-faulty replica will commit at F+1 or more non-faulty replicas eventually.
If some replica misses messages that were discarded by all non-faulty replicas, it will need to be brought up to date by transferring all or a portion of the service state. Therefore, replicas need some proof that the state is correct. These proofs are generated periodically using the checkpointing protocol, when a request with a sequence number divisible by some constant (e.g., 100) is executed. The checkpoint protocol is also used to advance the low and high water marks (which limit what messages will be accepted).

Of course PBFT still has a high communication cost, due to the all-to-all communications in the prepare and commit phases. Recent work on BFT protocols employ threshold signatures and are able to avoid these all-to-all broadcasts in the PBFT protocol, and replace them with leader to quorum and quorum to leader communications. That leads to a big improvement and makes the BFT protocol the same order of magnitude communication complexity as primary backup-replication and Paxos protocols. With pipelining and rotation of leaders, these modern BFT protocols achieve much better performance.
The serpentine history of Byzantine fault-tolerance
The paper starts with this declaration:"We believe that Byzantine fault-tolerant algorithms will be increasingly important in the future because malicious attacks and software errors are increasingly common and can cause faulty nodes to exhibit arbitrary behavior."How prescient of them. When Byzantine fault tolerance (BFT) was first introduced by Lamport in 1982, it was mostly of theoretical interest, and it remained so for a long time. Although the prediction in this 1999 paper eventually came true, I don't think it happened due to the reasons the paper expected it to happen. The paper gave the following boiler-plate justification of why BFT may become practical and relevant:
"Since malicious attacks and software errors can cause faulty nodes to exhibit Byzantine (i.e., arbitrary) behavior, Byzantine-fault-tolerant algorithms are increasingly important."This justification has been used by many papers, but I am not very fond of this argument. First of all, this argument desperately asks for a citation right? (The journal version of the paper, which came a couple years later, also does not provide a citation.) How do we know the malicious attacks and software failure modes map nicely and practically to Byzantine fault-model? It is a big assumption that a software bug, or an operator error, or a cracker that gets root on some machines can only affect upto 1/3rd of the nodes. In practice that is often not the case, as those faults are all correlated. A software bug in one replica will be present in the other replicas as well, and likely to manifest itself with the same state and input (the state-machine-replication approach is especially prone to this correlated failure). A cracker that broke into one replica is likely to use the same techniques or passwords to break into the other replicas.
Use of techniques like N-version programming may help alleviate the issue. The idea is to implement the same API/specifications in multiple different ways, so that a software error does not constitute a problem for more than one third of the replicas. But this is not easy, also not always effective. Many developers are prone to make similar mistakes/bugs in similar tricky places.
While there has been a decade of followup work to PBFT, since the above problems remained unaddressed, there was also a growing criticism of BFT work. I swear I have seen a couple talks toward 2010 that declared BFT impractical. They had titles like "Do we need BFT" and "BFT is impractical". Unfortunately I cannot find those talks now.
In the last five years or so, with the prominence of blockchains and adversarial commerce applications, BFT assumption/model became relevant again. Therefore, yes, the prediction in the opening of the paper turned out to be appropriate after all.
PBFT Protocol overview
The PBFT protocol introduced in this paper has improved significantly on previous work on BFT protocols. The previous BFT algorithms assumed a synchronous system and/or were too costly in terms of communication. The PBFT protocol introduced in this paper was the first to work in a partially synchronous environment (and to preserve safety in an asynchronous environment) and offered significant reductions in communication costs. The former is achieved through the use of views and view-changing, and the latter is achieved through the use of cryptography to authenticate messages and prevent spoofing and replays.PBFT is based on replicated state machine (RSM) approach. This is very similar to how Paxos uses RSM to achieve consensus to the face of crash faults. Here, due to Byzantine fault-tolerance, the protocol gets a bit more involved. Also instead of N=2F+1 in Paxos, BFT requires N=3F+1, where F is the upper bound on the number of faulty replicas, and N is the number of replicas in total. The reason is as follows. We cannot wait reply from more than N-F replicas, because the F faulty replicas may not reply. But what if the among the N-F replicas that respond, F of them are faulty replicas? So there must still be enough responses that those from non-faulty replicas outnumber those from faulty ones, i.e., N-2F>F.
The RSM maintenance works pretty similar to Paxos, or rather, viewstamped replication flavor of consensus. The replicas move through a succession of configurations called views (this corresponds to the ballotnumber concept in Paxos). In a view one replica is the primary and the others are followers.
Views are numbered consecutively. The primary of a view is replica p such that p= v mod N. View changes are carried out when it appears that the primary has failed.
The state of each replica includes the state of the service, a message log containing messages the replica has accepted, and an integer v denoting the replica's current view.
PBFT normal operation goes as follows:
1. A client sends a request to invoke a service operation to the primary
2. The primary multicasts the request to the backups
3. Replicas execute the request and send a reply to the client
4. The client waits for F+1 replies from different replicas with the same result; this is the result of the operation

Here the primary is replica 0. There are three phases to commit the request. The pre-prepare and prepare phases are used to totally order requests sent in the same view even when the primary, which proposes the ordering of requests, is faulty. The prepare and commit phases are used to ensure that requests that commit are totally ordered across views.
Pre-prepare phase
The primary assigns a sequence number to the request, adds its view v, multicasts a pre-prepare message to all the backups, and appends the message to its log.A backup accepts a pre-prepare message provided:
- the signatures in the request and the pre-prepare message are correct
- it is in view v
- it has not accepted a pre-prepare message for view and sequence number containing a different digest
- the sequence number in the pre-prepare message is between a low water mark, h, and a high water mark, H
Prepare phase
Accepting the pre-prepare message, a follower enters the prepare phase by multicasting a Prepare message to all other replicas and adds both messages to its log.A replica (including the primary) accepts prepare messages and adds them to its log provided their signatures are correct, their view number equals the replica’s current view, and their sequence number is between h and H.
The predicate, Prepared (m,v,n,i) holds iff replica i has inserted in its log:
- the request m
- a pre-prepare for m in view v with sequence number n, and
- 2F prepares from different backups that match the pre-prepare
Commit phase
Replica i multicasts a Commit message to other replicas when Prepared is truthified. Replicas accept commit messages and insert them in their log provided they are properly signed, the view number in the message is equal to the replica's current view, and the sequence number is between h and HThe predicated Committed (m,v,n) holds iff Prepared (m,v,n,i) is true for all i in some set of F+1 replicas. And the predicate Committed-local (m,v,n,i) holds iff Prepared (m,v,n,i) is true and i has accepted 2F+1 commits (possibly including its own) matching m.
As an invariant of PBFT, we have that if Committed-local (m,v,n,i) holds, then Committed (m,v,n) holds. This ensures that non-faulty replicas agree on the sequence numbers of requests that commit locally even if they commit in different views at each replica. Furthermore, with the view change protocol this ensures that any request that commits locally at a non-faulty replica will commit at F+1 or more non-faulty replicas eventually.
Garbage collection and checkpointing
For the safety condition to hold, messages must be kept in a replica's log until it knows that the requests they concern have been executed by at least F+1 non-faulty replicas and it can prove this to others in view changes.If some replica misses messages that were discarded by all non-faulty replicas, it will need to be brought up to date by transferring all or a portion of the service state. Therefore, replicas need some proof that the state is correct. These proofs are generated periodically using the checkpointing protocol, when a request with a sequence number divisible by some constant (e.g., 100) is executed. The checkpoint protocol is also used to advance the low and high water marks (which limit what messages will be accepted).
View-change
That was normal operation with a stable primary. The view-change protocol provides liveliness by allowing the system to make progress when the primary fails. View changes are triggered by timeouts that prevent followers from waiting indefinitely for requests to execute. Below is the essence of the view-change protocol.
Conclusion
Using PBFT, the paper shows how to implement a Byzantine-fault-tolerant NFS service. The paper performs evaluations on this service and shows that it is only 3% slower than a standard unreplicated NFS.Of course PBFT still has a high communication cost, due to the all-to-all communications in the prepare and commit phases. Recent work on BFT protocols employ threshold signatures and are able to avoid these all-to-all broadcasts in the PBFT protocol, and replace them with leader to quorum and quorum to leader communications. That leads to a big improvement and makes the BFT protocol the same order of magnitude communication complexity as primary backup-replication and Paxos protocols. With pipelining and rotation of leaders, these modern BFT protocols achieve much better performance.





Comments