TUX2: Distributed Graph Computation for Machine Learning
The TUX2 paper appeared in NSDI 17 and was authored by Wencong Xiao, Beihang University and Microsoft Research; Jilong Xue, Peking University and Microsoft Research; Youshan Miao, Microsoft Research; Zhen Li, Beihang University and Microsoft Research; Cheng Chen and Ming Wu, Microsoft Research; Wei Li, Beihang University; Lidong Zhou, Microsoft Research.
TUX2 introduces some new concepts to graph process engines to adapt them better for machine learning (ML) training jobs. Before I can talk about the contributions of TUX2, you need to bear with me as I explain how current graph processing frameworks fall short for ML training.
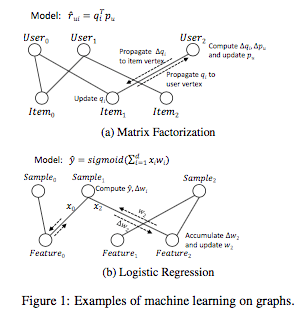
A topic-modeling algorithm like Latent Drichlet Allocation (LDA) can be modeled as a document-word graph. If a document contains a word, there is an edge between them; the data on that edge are the topics of the word in the document. Even logistic regression can be modeled as a sample-feature graph.
2. For ML computation, an iteration of a graph computation might involve multiple rounds of propagation between different types of vertices, rather than a simple series of GAS phases. The standard GAS model is unable to express such computation patterns efficiently.
3. Machine learning frameworks have been shown to benefit from the Stale Synchronous Parallel (SSP) model, a relaxed consistency model with bounded staleness to improve parallelism. The graph processing engines use Bulk Synchronous Parallel (BSP) model by default.
1. supports heterogeneity in the data model,
2. advocates a new graph model, MEGA (Mini-batch, Exchange, GlobalSync, and Apply), that allows flexible composition of stages, and
3. supports SSP in execution scheduling.
Next we discuss the basic design elements in TUX2, and how the above 3 capabilities are built on them.
Vertex-cut is very useful for implementing the parameter-server model: The master versions of all vertices' data can be treated as the distributed global state stored in a parameter server. The mirrors are distributed to workers, which also has the second type of vertices and use the mirror vertices to iterate on these second type of vertices.
Wait, the second type of vertices? Yes, here we harken back to the bipartite graph model. Recall that we had bipartite graph with heterogeneous vertices, with some vertices having higher degrees. Those higher degree vertices are master vertices and held at the server, and the low degree vertices are data/training for those master vertices and they cache the master vertices as mirror vertices and train on them. And, in some sense, the partitions of low-order vertex type in the bipartite graph corresponds to mini-batch.
The paper has the following to say on this. In a bipartite graph, TUX2 can enumerate all edges by scanning only vertices of one type. The choice of which type to enumerate sometimes has significant performance implications. Scanning the vertices with mirrors in a mini-batch tends to lead to a more efficient synchronization step, because these vertices are placed contiguously in an array. In contrast, if TUX2 scans vertices without mirrors in a mini-batch, the mirrors that get updated for the other vertex type during the scan will be scattered and thus more expensive to locate. TUX2 therefore allows users to specify which set of vertices to enumerate during the computation.
Each partition is managed by a process that logically plays both

Figure 3 illustrates how TUX2 organizes vertex data for a bipartite graph, using MF on a user-item graph as an example. Because user vertices have much smaller degree in general, only item vertices are split by vertex-cut partitioning. Therefore, a master vertex array in the server role contains only item vertices, and the worker role only manages user vertices. This way, there are no mirror replicas of user vertices and no distributed synchronization is needed. In the worker role, the mirrors of item and user vertices are stored in two separate arrays.
In each partition, TUX2 maintains vertices and edges in separate arrays. Edges in the edge array are grouped by source vertex. Each vertex has an index giving the offset of its edge-set in the edge array. Each edge contains information such as the id of the partition containing the destination vertex and the index of that vertex in the corresponding vertex array. This graph data structure is optimized for traversal and outperforms vertex indexing using a lookup table. Figure 2 shows how data are partitioned, stored, and assigned to execution roles in TUX2.

TUX2 supports SSP in the mini-batch granularity. It tracks the progress of each mini-batch iteration to enable computation of clocks. A worker considers clock t completed if the corresponding mini-batch is completed on all workers (including synchronizations between masters and mirrors) and if the resulting update has been applied to and reflected in the state. A worker can execute a task at clock t only if it knows that all clocks up to t−s−1 have completed, where s is the allowed slack.
MEGA allows users to construct an arbitrary sequence of stages. Unlike GAS, which needs to be repeated in order (i.e., GAS-GAS-GAS-GAS), in MEGA you can flexibly mix and match (e.g., E-A-E-A-G). For example, in algorithms such as MF and LDA, processing an edge involves updating both vertices. This requires two GAS phases, but can be accomplished in one Exchange phase in META. For LR, the vertex data propagations in both directions should be followed by an Apply phase, but no Scatter phases are necessary; this can be avoided in the MEGA model because MEGA allows an arbitrary sequence of stages.
Below are examples of Matrix factorization (MF) and Latent Dirichlet Allocation (LDA) programmed with the META model. (LDA's stage sequence is the same as MF's.)


The evaluations show that data layout matters greatly in the performance of ML algorithms. Figure 8 compares the performance of BlockPG, MF, and LDA with two different layouts: one an array-based graph data layout in TUX2 and the other a hash-table-based lay-out often used in parameter-server-based systems (but implemented in TUX2 for comparison). The y-axis is the average running time of one iteration for BlockPG, and of 10 iterations for MF and LDA to show the numbers on a similar scale. These results show that the graph layout improves performance by up to 2.4× over the hash-table-based layout.

The paper also includes a comparison with Petuum, but the evaluations have several caveats. The evaluations do not include comparison of convergence/execution time; execution time per iteration does not always determine the convergence time. The evaluations do not take into account the partitioning time of the graph for TUX2. And finally, some comparisons used early unpatched version of Petuum MF algorithm whose data placement issues are resolved later.
I like this paper; it made me ask and ponder on many questions, which is good.
I don't think TUX2 pushes the state of the art in ML. ML processing frameworks are already very efficient and general with the iterative parameter-server computing model, and they are getting better and more fine grained.
On the other hand, I think TUX2 is valuable because it showed how the high-level graph computing frameworks can be adapted to implement the low-level parameter-server approach and address ML training problems more efficiently. This may provide some advantages for problems that are/need to be represented as graphs, such as for performing ML training on Sparql data stores.
Moreover by using higher-level primitives, TUX2 provides some ease of programmability. I guess this may be leveraged further to achieve some plug and play programming of ML for certain class of programs.
So I find this to be a conceptually very satisfying paper as it bridges the graph processing model to parameter-server model. I am less certain about the practicality part.
2. How does graph processing frameworks compare with dataflow frameworks?
There are big differences between dataflow frameworks and graph processing frameworks. In the dataflow model, there is a symbolic computation graph, the graph nodes represent mathematical operations, while the graph edges represent the data that flow between the operations. That is a very different model than the graph processing model here.
In MEGA, there are only 4 stages, where the Apply stage can take in user defined functions. This is higher-level (and arguably more programming friendly) than a dataflow framework such as TensorFlow which has many hundreds of predefined operators as vertices.
3. How does TUX2 apply to Deep Learning (DL)?
The paper does not talk about whether TUX2 can apply to DL and how it can apply.
It may be possible to make DL fit the TUX2 model with some stretching. Deep neural network (DNN) layers (horizontally or vertically partitioned) could be the high-rank vertices hold in the servers. And the images are low-ranked vertices hold in partitions.
But this will require treating the DNN partions as a meta-vertex and schedule executions for each sub-vertes in the meta-vertex in one cycle. I have no clue about how to make backpropagation work here though.
Moreover, for each image, the image may need to link to entire NN, so the bipartite graph may collapse into a trivial one and trivial data-parallelism. It may be possible to make the convolutional layers can be distributed. It may even be possible to insert early exits and train that way.
So, it may be possible but it is certainly not straightforward. I am not even touching the subject of the performance of such a system.
TUX2 introduces some new concepts to graph process engines to adapt them better for machine learning (ML) training jobs. Before I can talk about the contributions of TUX2, you need to bear with me as I explain how current graph processing frameworks fall short for ML training.
Background and motivation
Graph processing engines often takes a "think like a vertex" approach. A dominant computing model in "think like a vertex" approach is the Gather-Apply-Scatter (GAS) model. You can brush up on graph processing engines by reading my reviews of Pregel and Facebook graph processing.Modeling ML problems as bipartite graphs
Many ML problems can be modeled with graphs and attacked via iterative computation on the graph vertices. The Matrix Factorization (MF) algorithm, used in recommendation systems, can be modeled as a computation on a bipartite user-item graph where each vertex corresponds to a user or an item and each edge corresponds to a user's rating of an item.A topic-modeling algorithm like Latent Drichlet Allocation (LDA) can be modeled as a document-word graph. If a document contains a word, there is an edge between them; the data on that edge are the topics of the word in the document. Even logistic regression can be modeled as a sample-feature graph.

Gaps in addressing ML via graph processing
1. The graphs that model ML problems often have bi-partite nature and heterogeneous vertices, with distinct roles (e.g., user vertices and item vertices). However, the standard graph model used in graph processing frameworks assumes a homogeneous set of vertices.2. For ML computation, an iteration of a graph computation might involve multiple rounds of propagation between different types of vertices, rather than a simple series of GAS phases. The standard GAS model is unable to express such computation patterns efficiently.
3. Machine learning frameworks have been shown to benefit from the Stale Synchronous Parallel (SSP) model, a relaxed consistency model with bounded staleness to improve parallelism. The graph processing engines use Bulk Synchronous Parallel (BSP) model by default.
TUX2 Design
To address the gaps identified above, TUX21. supports heterogeneity in the data model,
2. advocates a new graph model, MEGA (Mini-batch, Exchange, GlobalSync, and Apply), that allows flexible composition of stages, and
3. supports SSP in execution scheduling.
Next we discuss the basic design elements in TUX2, and how the above 3 capabilities are built on them.
The vertex-cut approach
TUX2 uses the vertex-cut approach (introduced in PowerGraph), where the edge set of a high-degree vertex can be split into multiple partitions, each maintaining a replica of the vertex. One of these replicas is designated the master; it maintains the master version of the vertex's data. All the remaining replicas are called mirrors, and each maintains a local cached copy.Vertex-cut is very useful for implementing the parameter-server model: The master versions of all vertices' data can be treated as the distributed global state stored in a parameter server. The mirrors are distributed to workers, which also has the second type of vertices and use the mirror vertices to iterate on these second type of vertices.
Wait, the second type of vertices? Yes, here we harken back to the bipartite graph model. Recall that we had bipartite graph with heterogeneous vertices, with some vertices having higher degrees. Those higher degree vertices are master vertices and held at the server, and the low degree vertices are data/training for those master vertices and they cache the master vertices as mirror vertices and train on them. And, in some sense, the partitions of low-order vertex type in the bipartite graph corresponds to mini-batch.
The paper has the following to say on this. In a bipartite graph, TUX2 can enumerate all edges by scanning only vertices of one type. The choice of which type to enumerate sometimes has significant performance implications. Scanning the vertices with mirrors in a mini-batch tends to lead to a more efficient synchronization step, because these vertices are placed contiguously in an array. In contrast, if TUX2 scans vertices without mirrors in a mini-batch, the mirrors that get updated for the other vertex type during the scan will be scattered and thus more expensive to locate. TUX2 therefore allows users to specify which set of vertices to enumerate during the computation.
Each partition is managed by a process that logically plays both
- a worker role, to enumerate vertices in the partition and propagate vertex data along edges, and
- a server role, to synchronize states between mirror vertices and their corresponding masters.

Figure 3 illustrates how TUX2 organizes vertex data for a bipartite graph, using MF on a user-item graph as an example. Because user vertices have much smaller degree in general, only item vertices are split by vertex-cut partitioning. Therefore, a master vertex array in the server role contains only item vertices, and the worker role only manages user vertices. This way, there are no mirror replicas of user vertices and no distributed synchronization is needed. In the worker role, the mirrors of item and user vertices are stored in two separate arrays.
In each partition, TUX2 maintains vertices and edges in separate arrays. Edges in the edge array are grouped by source vertex. Each vertex has an index giving the offset of its edge-set in the edge array. Each edge contains information such as the id of the partition containing the destination vertex and the index of that vertex in the corresponding vertex array. This graph data structure is optimized for traversal and outperforms vertex indexing using a lookup table. Figure 2 shows how data are partitioned, stored, and assigned to execution roles in TUX2.

Scheduling minibatches with SSP
TUX2 executes each iteration on a minibatch with a specified size. Each worker first chooses a set of vertices or edges as the current minibatch to execute on. After the execution on the mini-batch finishes, TUX2 acquires another set of vertices or edges for the next minibatch, often by continuing to enumerate contiguous segments of vertex or edge arrays.TUX2 supports SSP in the mini-batch granularity. It tracks the progress of each mini-batch iteration to enable computation of clocks. A worker considers clock t completed if the corresponding mini-batch is completed on all workers (including synchronizations between masters and mirrors) and if the resulting update has been applied to and reflected in the state. A worker can execute a task at clock t only if it knows that all clocks up to t−s−1 have completed, where s is the allowed slack.
The MEGA model
TUX2 introduces a new stage-based MEGA model, where each stage is a computation on a set of vertices and their edges in a graph. Each stage has user-defined functions (UDF) to be applied on the vertices or edges accessed during it. MEGA defines four types of stage: Mini-batch, Exchange, GlobalSync, and Apply.MEGA allows users to construct an arbitrary sequence of stages. Unlike GAS, which needs to be repeated in order (i.e., GAS-GAS-GAS-GAS), in MEGA you can flexibly mix and match (e.g., E-A-E-A-G). For example, in algorithms such as MF and LDA, processing an edge involves updating both vertices. This requires two GAS phases, but can be accomplished in one Exchange phase in META. For LR, the vertex data propagations in both directions should be followed by an Apply phase, but no Scatter phases are necessary; this can be avoided in the MEGA model because MEGA allows an arbitrary sequence of stages.
Below are examples of Matrix factorization (MF) and Latent Dirichlet Allocation (LDA) programmed with the META model. (LDA's stage sequence is the same as MF's.)


Implementation and Evaluation
TUX2 is implemented in ~12,000 lines of C++ code. TUX2 takes graph data in a collection of text files as input. Each process picks a separate subset of those files and performs bipartite-graph-aware algorithms to partition the graph in a distributed way. Each partition is assigned to, and stored locally with, a process. Unfortunately the evaluations with TUX2 do not take into account graph partitioning time, which can be very high.The evaluations show that data layout matters greatly in the performance of ML algorithms. Figure 8 compares the performance of BlockPG, MF, and LDA with two different layouts: one an array-based graph data layout in TUX2 and the other a hash-table-based lay-out often used in parameter-server-based systems (but implemented in TUX2 for comparison). The y-axis is the average running time of one iteration for BlockPG, and of 10 iterations for MF and LDA to show the numbers on a similar scale. These results show that the graph layout improves performance by up to 2.4× over the hash-table-based layout.

The paper also includes a comparison with Petuum, but the evaluations have several caveats. The evaluations do not include comparison of convergence/execution time; execution time per iteration does not always determine the convergence time. The evaluations do not take into account the partitioning time of the graph for TUX2. And finally, some comparisons used early unpatched version of Petuum MF algorithm whose data placement issues are resolved later.
MAD questions
1. What is the net gain here?I like this paper; it made me ask and ponder on many questions, which is good.
I don't think TUX2 pushes the state of the art in ML. ML processing frameworks are already very efficient and general with the iterative parameter-server computing model, and they are getting better and more fine grained.
On the other hand, I think TUX2 is valuable because it showed how the high-level graph computing frameworks can be adapted to implement the low-level parameter-server approach and address ML training problems more efficiently. This may provide some advantages for problems that are/need to be represented as graphs, such as for performing ML training on Sparql data stores.
Moreover by using higher-level primitives, TUX2 provides some ease of programmability. I guess this may be leveraged further to achieve some plug and play programming of ML for certain class of programs.
So I find this to be a conceptually very satisfying paper as it bridges the graph processing model to parameter-server model. I am less certain about the practicality part.
2. How does graph processing frameworks compare with dataflow frameworks?
There are big differences between dataflow frameworks and graph processing frameworks. In the dataflow model, there is a symbolic computation graph, the graph nodes represent mathematical operations, while the graph edges represent the data that flow between the operations. That is a very different model than the graph processing model here.
In MEGA, there are only 4 stages, where the Apply stage can take in user defined functions. This is higher-level (and arguably more programming friendly) than a dataflow framework such as TensorFlow which has many hundreds of predefined operators as vertices.
3. How does TUX2 apply to Deep Learning (DL)?
The paper does not talk about whether TUX2 can apply to DL and how it can apply.
It may be possible to make DL fit the TUX2 model with some stretching. Deep neural network (DNN) layers (horizontally or vertically partitioned) could be the high-rank vertices hold in the servers. And the images are low-ranked vertices hold in partitions.
But this will require treating the DNN partions as a meta-vertex and schedule executions for each sub-vertes in the meta-vertex in one cycle. I have no clue about how to make backpropagation work here though.
Moreover, for each image, the image may need to link to entire NN, so the bipartite graph may collapse into a trivial one and trivial data-parallelism. It may be possible to make the convolutional layers can be distributed. It may even be possible to insert early exits and train that way.
So, it may be possible but it is certainly not straightforward. I am not even touching the subject of the performance of such a system.



Comments