Learning Machine Learning: Multinomial Logistic Classification
In the previous post, we got started on classification. Classification is the task of taking an input and giving it a label that says, this is an "A". In the previous post, we covered logistic regression, which made the decision for a single label "A". In this post, we will generalize that to multinomial logistic classification where your job is to figure out which of the K classes a given input belongs to.
For this post I follow the course notes from the Udacity Deep Learning Class by Vincent Vanhoucke at Google. I really liked his presentation of the course: very practical and to the point. This must have required a lot of preparation. Going through the video transcript file, I can see that the material has been prepared meticulously to be clear and concise. I strongly recommend the course.
The course uses TensorFlow to teach you about Deep Neural Networks in a hands-on manner, and follows the MNIST letter recognition example in the first three lessons. Don't get stressed about TensorFlow installation and getting the tutorial environment setup. It is as easy as downloading a Docker container, and going to your browser to start filling in Jupyter Notebooks. I enjoyed programming in the Jupyter Notebooks a lot. Jupyter Notebooks is literate programming ...um, literally.
Of course, we need to first train our model (W and b that is) using the training data and the corresponding training labels to figure out the optimal W and b to fit the training data. Each image, that we have as an input can have one and only one possible label. So, we're going to turn the scores (aka logits) the model outputs into probabilities. While doing so, we want the probability of the correct class to be very close to one and the probability for every other class to be close to zero.
This is how multinomial logistic classification generalizes logistic regression.
def softmax(x):
"""Compute softmax values for each sets of scores in x."""
return np.exp(x)/np.sum(np.exp(x), axis=0)
Compare the softmax with the logistic function $g(z)= \frac{1}{(1 + e^{-z})}$ in the logistic regression post. The logistic function was concerned with deciding if the output is label "A" or not (less than 0.5 and it is not A, and more than 0.5 it is A), whereas the softmax function is giving/distributing probabilities for the output being in each of the output class "A", "B", "C", etc., the sum of which adds up to 1.
One-hot encoding is a way to represent the labels mathematically. Each label will be represented by a vector of size output classes and it has the value 1.0 for the correct class and 0 every where else.
To measure the distance between those two probability vectors, *cross-entropy* is used. Denoting distance with D, Softmax(Y) with S, Label with L, the formula for cross-entropy is: $D(S,L)= -\sum_i L_i log(S_i)$.
When the $i$th entry corresponds to the correct class, $L_i=1$, and the cost (i.e., distance) becomes -log(S_i). If $S_i$ has a larger probability close to 1, the cost becomes lower, and if $S_i$ has a lower probability close to 0, the cost becomes larger. In other words, the cross entropy function penalizes $S_i$ for the false-negatives. When the $i$th entry corresponds to one of the incorrect classes, $L_i=0$ and the entry in $S_i$ becomes irrelevant for the cost. So the cross entropy function does not penalize $S_i$ for the false positives.
Compare the cross-entropy with the cost function in logistic regression:
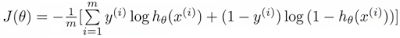
It looks like the cross-entropy does not take into account false-positives, whereas the earlier $J$ cost function took both into account and penalized both the false-positives and false-negatives. On the other hand, cross-entropy does consider false-positives in an indirect fashion: Since the softmax is a zero-sum probability classifier, improving it for the false-negatives does take care of the false-positives.
We want to minimize this training loss function, and we know that a simple way to do that is via gradient descent. Take the derivative of your loss, with respect to your parameters, and follow that derivative by taking a step downwards and repeat until you get to the bottom.
As we discussed before, in order to speed up gradient descent, normalization is important. Normalization is simple, if you are dealing with images. You can take the pixel values of your image, they are typically between 0 and 255. And simply subtract 128 and divide by 128. W and b should also be initialized for the gradient descent to proceed. Draw the weights randomly from a Gaussian distribution with mean zero and a small standard deviation sigma.
How small should an SGD step (aka "learning rate") be? This is an involved question: setting the learning rate large doesn't make learning faster, instead using large steps may miss the optima valley, and may even cause divergence. To set a suitable value for learning rate, we can try a range of values 0.001, 0.003, 0.01, 0.03. 0.1, 0.3, and plot convergence. After you settle on a suitable step size to start with, another useful thing is to make the step smaller and smaller as the training progresses during a training run, for example by applying an exponential decay. AdaGrad helps here. AdaGrad is a modification of SGD that makes learning less sensitive to hyperparameters (such as learning rate, momentum, decay).
1-layer NN works like this:
In the next post, we will learn about adding hidden layers via rectified linear units (ReLUs) to build deeper NNs. Deeper NNs are able to capture more complex functions to fit the data better. For training the deep NN we will learn about how to backpropagate the gradient descent adjustments to the corresponding layers in the NN using the chain rule of derivation.
For this post I follow the course notes from the Udacity Deep Learning Class by Vincent Vanhoucke at Google. I really liked his presentation of the course: very practical and to the point. This must have required a lot of preparation. Going through the video transcript file, I can see that the material has been prepared meticulously to be clear and concise. I strongly recommend the course.
The course uses TensorFlow to teach you about Deep Neural Networks in a hands-on manner, and follows the MNIST letter recognition example in the first three lessons. Don't get stressed about TensorFlow installation and getting the tutorial environment setup. It is as easy as downloading a Docker container, and going to your browser to start filling in Jupyter Notebooks. I enjoyed programming in the Jupyter Notebooks a lot. Jupyter Notebooks is literate programming ...um, literally.
Multinomial logistic classification
The logistic classifier takes an input vector X (for example, the pixels in an image), and applies a linear function to them to generate its predictions. The linear function is just a giant matrix multiply: it multiplies X with the weights matrix, W, and add biases, b, to generate its prediction to be one of the output classes.Of course, we need to first train our model (W and b that is) using the training data and the corresponding training labels to figure out the optimal W and b to fit the training data. Each image, that we have as an input can have one and only one possible label. So, we're going to turn the scores (aka logits) the model outputs into probabilities. While doing so, we want the probability of the correct class to be very close to one and the probability for every other class to be close to zero.
This is how multinomial logistic classification generalizes logistic regression.
- We use a softmax function to turn the scores the model outputs into probabilities.
- We then use cross entropy function as our loss function compare those probabilities to the one-hot encoded labels.
Softmax function and one-hot encoding
A softmax function, S, is of the form $S(y_i)=\frac{e^{y_i}}{\sum e^{y_j}}$. This way S can take any kind of scores and turn them into proper probabilities which sum to 1.def softmax(x):
"""Compute softmax values for each sets of scores in x."""
return np.exp(x)/np.sum(np.exp(x), axis=0)
Compare the softmax with the logistic function $g(z)= \frac{1}{(1 + e^{-z})}$ in the logistic regression post. The logistic function was concerned with deciding if the output is label "A" or not (less than 0.5 and it is not A, and more than 0.5 it is A), whereas the softmax function is giving/distributing probabilities for the output being in each of the output class "A", "B", "C", etc., the sum of which adds up to 1.
One-hot encoding is a way to represent the labels mathematically. Each label will be represented by a vector of size output classes and it has the value 1.0 for the correct class and 0 every where else.
Cross entropy
We can now measure the accuracy of the model by simply comparing two vectors: one is the softmax vector that comes out of the classifiers and contains the probabilities of the classes, and the other one is the one-hot encoded vector that corresponds to the label.To measure the distance between those two probability vectors, *cross-entropy* is used. Denoting distance with D, Softmax(Y) with S, Label with L, the formula for cross-entropy is: $D(S,L)= -\sum_i L_i log(S_i)$.
When the $i$th entry corresponds to the correct class, $L_i=1$, and the cost (i.e., distance) becomes -log(S_i). If $S_i$ has a larger probability close to 1, the cost becomes lower, and if $S_i$ has a lower probability close to 0, the cost becomes larger. In other words, the cross entropy function penalizes $S_i$ for the false-negatives. When the $i$th entry corresponds to one of the incorrect classes, $L_i=0$ and the entry in $S_i$ becomes irrelevant for the cost. So the cross entropy function does not penalize $S_i$ for the false positives.
Compare the cross-entropy with the cost function in logistic regression:
It looks like the cross-entropy does not take into account false-positives, whereas the earlier $J$ cost function took both into account and penalized both the false-positives and false-negatives. On the other hand, cross-entropy does consider false-positives in an indirect fashion: Since the softmax is a zero-sum probability classifier, improving it for the false-negatives does take care of the false-positives.
Minimizing Cross Entropy via Gradient Descent
To transform the multinomial classification problem into a proper optimization problem, we define training loss to measure the cross-entropy averaged over the entire training sets for all the training inputs and the corresponding training labels: $\mathcal{L} = 1/N * \sum_i D( S(Wx_i+b), L_i)$We want to minimize this training loss function, and we know that a simple way to do that is via gradient descent. Take the derivative of your loss, with respect to your parameters, and follow that derivative by taking a step downwards and repeat until you get to the bottom.
As we discussed before, in order to speed up gradient descent, normalization is important. Normalization is simple, if you are dealing with images. You can take the pixel values of your image, they are typically between 0 and 255. And simply subtract 128 and divide by 128. W and b should also be initialized for the gradient descent to proceed. Draw the weights randomly from a Gaussian distribution with mean zero and a small standard deviation sigma.
Stochastic Gradient Descent
Computing gradient descent using every single element in your training set can involve a lot of computation if your data set is big. And since gradient descent is iterative, this needs to get repeated until convergence. It is possible to improve performance by simply computing the average loss for a very small random fraction of the training data. This technique is called stochastic gradient descent, SGD. SGD is used a lot for deep learning because it scales well with both data and model size.How small should an SGD step (aka "learning rate") be? This is an involved question: setting the learning rate large doesn't make learning faster, instead using large steps may miss the optima valley, and may even cause divergence. To set a suitable value for learning rate, we can try a range of values 0.001, 0.003, 0.01, 0.03. 0.1, 0.3, and plot convergence. After you settle on a suitable step size to start with, another useful thing is to make the step smaller and smaller as the training progresses during a training run, for example by applying an exponential decay. AdaGrad helps here. AdaGrad is a modification of SGD that makes learning less sensitive to hyperparameters (such as learning rate, momentum, decay).
How do we go deep?
We devised a neural network (NN) with just 1-layer, the output layer. Our1-layer NN works like this:
- It multiplies training data by W matrix and adds b
- It applies the softmax and then cross entropy loss to calculate the average of this loss over the entire training data.
- It uses SGD to compute the derivative of this loss with respect to W and b, and applies the $\delta$ adjustment to W and b (i.e., takes a step downwards in the gradient field)
- It keeps repeating the process until it converges to a minimum of the loss function.
In the next post, we will learn about adding hidden layers via rectified linear units (ReLUs) to build deeper NNs. Deeper NNs are able to capture more complex functions to fit the data better. For training the deep NN we will learn about how to backpropagate the gradient descent adjustments to the corresponding layers in the NN using the chain rule of derivation.



Comments