Paper summary: Detecting global predicates in distributed systems with clocks
This is a 2000 paper by Scott Stoller. The paper is about detecting global predicates in distributed systems.
There has been a lot of previous work on predicate detection (e.g., Marzullo & Neiger WDAG 1991, Verissimo 1993), but those work considered vector clock (VC) timestamped events sorted via happened-before (hb) relationship. This paper proposes a framework for predicate detection over events timestamped with approximately-synchronized (think NTP) physical-time (PT) clocks.
This was a tough/deep paper to read and a rewarding one as well. I think this paper should receive more interest from distributed systems developers as it has applications to the cloud computing monitoring services. As you can see in Facebook stack and Google stack, monitoring services are an indispensible component of large-scale cloud computing systems.
It turns out that using PT also provides benefits over using VC in terms of complexity of predicate detection. The worst case complexity for predicated detection using hb captured by VC is Ω(EN), where E is the maximum number of events executed by each process, and N is the number of processes. On the other hand, the smaller the uncertainties in events' PT timestamps, i.e., the less the events overlap, the cheaper the PT-based predicate detection gets. With some assumptions on the inter-event spacing being larger than time synchronization uncertainty, it is possible to have worst-case time complexity for PT-based predicate detection to be O(3N E N2) --- linear in E.
I will say more on this point and how using our hybrid clocks can further reduce cost of predicate detection at the end of this post.
Each event e has an interval timestamp its(e), which is an interval with lower endpoint lwr(e) and upper endpoint upr(e). PT timestamping should satisfy the following conditions.
TS1: ∀ e: lwr(e) ≤ upr(e)
TS2: ∀ e1 with a succeeding event e2 on the same process: lwr(e1) ≤ lwr(e2) and upr(e1)≤ upr(e2)
TS3: ∀ e1,e2: if e1 occurred before e2 in real time, then lwr(e1) ≤ upr(e2)
TS3 is the strongest among these assumptions. Still this is a fairly general practical modeling of approximate time synchronization: The intervals of events do not need to be all equal across processes or even along the events on the same process.
The paper shows that CGS lattice theory is not specific to hb but applies to any partial generic ordering gb on events, that satisfy TS2. Two local states are concurrent if they are not related by gb. A global state is consistent with respect to gb if its constituent local states are pairwise concurrent.
consisgb (g) ≡ ∀ i, j: i ≠ j: \neg (g(i) gb g(j))
By adopting PT instead of VC for timestamping and ordering, the paper defines two ordering relations db ("definitely occurred before") and pb ("possibly occurred before") among events as follows.
e1 db e2 ≡ upr(e1) < lwr(e2)
e1 pb e2 ≡ ¬ (e2 db e1)
Notice how pb is elegantly defined in terms of db.
By substituting db and pb orderings in the generic CGS framework above, the paper obtains definitions of 3 distinct detection modalities: Poss-db θ (“θ possibly held”), Def-db θ (“θ definitely held”), and Inst θ (“θ definitely held at a specific instant”). We talk about these detection modalities and developing efficient detection algorithms for them in the next two sections.
As we mentioned in the beginning, the quality of time synchronization affect the cost of predicate detection. If the bounds on the offsets are comparable to or smaller than the mean interval between events that potentially truthify or falsify θ, then the number of global states that must be checked is comparable to the number of global states that the system actually passed through during execution, which is O(NE). In contrast, the number of global states considered in the asynchronous hb case is O(EN).
Assume the interval between consecutive events at a process is at least τ.
For Poss-db and Def-db worst-case time complexities are as follows:
- if τ > 2ε, O(3N E N2)
- if τ ≤ 2ε, O((4ε/τ +2){N-1} E N2)
This second option is the problematic zone. For τ << ε the time complexity of detection algorithm grows quickly. The figure below illustrates this, and shows how number of CGS change with respect to E and the ratio μ/ε, where μ is the mean inter-event time.

Substituting pb ordering in the generic theory of CGS, we get Poss-pb and Def-pb. In fact, pb collapses Def-pb and Pos-pb into one, Inst. This is because there are no alternate-paths in the pb computation. pb looks at inevitable global states, i.e., SCGS. The below computation has only two SCGSs (1,2) and (3,2).

This is similar to Properly detection by Fromentin and Raynal 1997. The computation contains O(NE) local states and there are only O(NE) SCGSs. And, the worst case time complexity of algorithm: O((N log N) E)
This is really low cost. So, where is the catch?
It turns out Inst detection is not enough/complete. Inst may miss some CGSs as illustrated below. (The paper doesn't explicitly discuss this, so this gave me some confusion before I could figure this out.)


But, going with VC becomes disadvantageous in many cases: when there isn't enough communication to introduce enough hb restrictions. PT can also become very disadvantageous: when μ/ε << 1. (Figure 6 shows how quickly number of CGSs to consider can grow in this region.)
Even worse, within the same system you can have VC become disadvantegous in some regions/phases of computation and PT in others. (You can have excited communication caused by closeby events within ε. So for ε in 10ms, you can have several regions where μ/ε to be <<1. This increases the complexity of Deff-db and Poss-db greatly. Especially for large N.)
We had recently introduced hybrid clocks, and in particular hybrid vector clocks (HVC). With HVC you don't have to choose one over another; HVC offers you the lowest cost detection of VC and PT at any point. Moreover while VC is of O(N) size, with HVC thanks to loosely-synchronized clock assumption it is possible to keep the sizes of HVC to be a couple entries at each process. HVC captures the communications in the timestamps and provides the best of VC and PT worlds.
We are investigating these issues with my colleague Sandeep Kulkarni at Michigan State, as part of our NSF supported project on highly auditable distributed systems.
It also looks like the db and pb relations should have applications to linearizability/serializability in distributed databases. And it will be interesting to investigate these further.
There has been a lot of previous work on predicate detection (e.g., Marzullo & Neiger WDAG 1991, Verissimo 1993), but those work considered vector clock (VC) timestamped events sorted via happened-before (hb) relationship. This paper proposes a framework for predicate detection over events timestamped with approximately-synchronized (think NTP) physical-time (PT) clocks.
This was a tough/deep paper to read and a rewarding one as well. I think this paper should receive more interest from distributed systems developers as it has applications to the cloud computing monitoring services. As you can see in Facebook stack and Google stack, monitoring services are an indispensible component of large-scale cloud computing systems.
Motivation
Using PT for timestamping (and predicate detection) has several advantages over using VC. VC is O(N), whereas PT is a scalar. For capturing hb, VC assumes that all communication occur in the present system and there are no backchannels, which is not practical for today's large-scale integrated system of systems. Using PT alleviates the backchannel problem: even if there is not direct communication path, if event B happened in physical time later than event A, then we can still identify that event A can affect event B due to out-of-bound communication. Finally, using PT for timestamping allows the devops to be able to query the system in relation to physical time, whereas VC fails to support it.It turns out that using PT also provides benefits over using VC in terms of complexity of predicate detection. The worst case complexity for predicated detection using hb captured by VC is Ω(EN), where E is the maximum number of events executed by each process, and N is the number of processes. On the other hand, the smaller the uncertainties in events' PT timestamps, i.e., the less the events overlap, the cheaper the PT-based predicate detection gets. With some assumptions on the inter-event spacing being larger than time synchronization uncertainty, it is possible to have worst-case time complexity for PT-based predicate detection to be O(3N E N2) --- linear in E.
I will say more on this point and how using our hybrid clocks can further reduce cost of predicate detection at the end of this post.
Computation model
A local computation has the form e1, s1, e2, s2, e3, s3, where the ei are events, and the si are local states. A global state of a distributed system is a collection of local states.Each event e has an interval timestamp its(e), which is an interval with lower endpoint lwr(e) and upper endpoint upr(e). PT timestamping should satisfy the following conditions.
TS1: ∀ e: lwr(e) ≤ upr(e)
TS2: ∀ e1 with a succeeding event e2 on the same process: lwr(e1) ≤ lwr(e2) and upr(e1)≤ upr(e2)
TS3: ∀ e1,e2: if e1 occurred before e2 in real time, then lwr(e1) ≤ upr(e2)
TS3 is the strongest among these assumptions. Still this is a fairly general practical modeling of approximate time synchronization: The intervals of events do not need to be all equal across processes or even along the events on the same process.
Generic theory of consistent global states (CGS)
A consistent global state (CGS) is a global cut that could have occurred during the computation.The paper shows that CGS lattice theory is not specific to hb but applies to any partial generic ordering gb on events, that satisfy TS2. Two local states are concurrent if they are not related by gb. A global state is consistent with respect to gb if its constituent local states are pairwise concurrent.
consisgb (g) ≡ ∀ i, j: i ≠ j: \neg (g(i) gb g(j))
By adopting PT instead of VC for timestamping and ordering, the paper defines two ordering relations db ("definitely occurred before") and pb ("possibly occurred before") among events as follows.
e1 db e2 ≡ upr(e1) < lwr(e2)
e1 pb e2 ≡ ¬ (e2 db e1)
Notice how pb is elegantly defined in terms of db.
By substituting db and pb orderings in the generic CGS framework above, the paper obtains definitions of 3 distinct detection modalities: Poss-db θ (“θ possibly held”), Def-db θ (“θ definitely held”), and Inst θ (“θ definitely held at a specific instant”). We talk about these detection modalities and developing efficient detection algorithms for them in the next two sections.
Detection based on strong event ordering, db
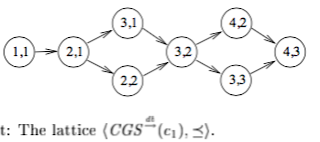
Substituting db ordering in the generic theory of CGS, we get Poss-db and Def-db. A computation satisfies Poss-db Q iff there exists some interleaving of events that is consistent with db and in which the system passes through a global state satisfying predicate Q. A computation satisfies Def-db Q iff for every interleaving of events that is consistent with db, Q holds. These two are analog to Poss-hb and Def-hb for the hb relation on the CGS framework. Figure 1 illustrates the nuance between Poss-db and Def-db. If Q holds only at CGS <3,1>, then Poss-db holds, but Def-db would not since computation might have taken <2,2> path instead of <3,1> path and Q does not hold at <2,2>. Def-db would hold if Q holds in both <3,1> and <2,2>. Or, instead if Q holds only at CGS <2,1>, then Def-db still holds.
As we mentioned in the beginning, the quality of time synchronization affect the cost of predicate detection. If the bounds on the offsets are comparable to or smaller than the mean interval between events that potentially truthify or falsify θ, then the number of global states that must be checked is comparable to the number of global states that the system actually passed through during execution, which is O(NE). In contrast, the number of global states considered in the asynchronous hb case is O(EN).
Assume the interval between consecutive events at a process is at least τ.
For Poss-db and Def-db worst-case time complexities are as follows:
- if τ > 2ε, O(3N E N2)
- if τ ≤ 2ε, O((4ε/τ +2){N-1} E N2)
This second option is the problematic zone. For τ << ε the time complexity of detection algorithm grows quickly. The figure below illustrates this, and shows how number of CGS change with respect to E and the ratio μ/ε, where μ is the mean inter-event time.

Detection based on weak event ordering, pb
In contrast to db, pb is a total order and not a partial order.Substituting pb ordering in the generic theory of CGS, we get Poss-pb and Def-pb. In fact, pb collapses Def-pb and Pos-pb into one, Inst. This is because there are no alternate-paths in the pb computation. pb looks at inevitable global states, i.e., SCGS. The below computation has only two SCGSs (1,2) and (3,2).

This is similar to Properly detection by Fromentin and Raynal 1997. The computation contains O(NE) local states and there are only O(NE) SCGSs. And, the worst case time complexity of algorithm: O((N log N) E)
This is really low cost. So, where is the catch?
It turns out Inst detection is not enough/complete. Inst may miss some CGSs as illustrated below. (The paper doesn't explicitly discuss this, so this gave me some confusion before I could figure this out.)


How would hybrid time/clocks benefit
In Stoller's world, you need to make a binary choice before hand: go either with VC- or PT- based timestamping and detection.But, going with VC becomes disadvantageous in many cases: when there isn't enough communication to introduce enough hb restrictions. PT can also become very disadvantageous: when μ/ε << 1. (Figure 6 shows how quickly number of CGSs to consider can grow in this region.)
Even worse, within the same system you can have VC become disadvantegous in some regions/phases of computation and PT in others. (You can have excited communication caused by closeby events within ε. So for ε in 10ms, you can have several regions where μ/ε to be <<1. This increases the complexity of Deff-db and Poss-db greatly. Especially for large N.)
We had recently introduced hybrid clocks, and in particular hybrid vector clocks (HVC). With HVC you don't have to choose one over another; HVC offers you the lowest cost detection of VC and PT at any point. Moreover while VC is of O(N) size, with HVC thanks to loosely-synchronized clock assumption it is possible to keep the sizes of HVC to be a couple entries at each process. HVC captures the communications in the timestamps and provides the best of VC and PT worlds.
We are investigating these issues with my colleague Sandeep Kulkarni at Michigan State, as part of our NSF supported project on highly auditable distributed systems.
It also looks like the db and pb relations should have applications to linearizability/serializability in distributed databases. And it will be interesting to investigate these further.


Comments