Analysis of Bounds on Hybrid Vector Clocks
This work is in collaboration with Sorrachai Yingchareonthawornchai and Sandeep Kulkarni at the Michigan State University and is currently under submission.
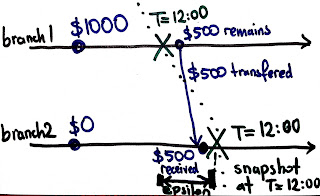
Practice of distributed systems employs loosely synchronized clocks, mostly using NTP. Unfortunately, perfect synchronization is unachievable due to messaging with uncertain latency, clock skew, and failures. These sync errors lead to anomalies. For example, a send event at Branch1 may be assigned a timestamp greater than the corresponding receive event at Branch2, because Branch1's clock is slightly ahead of Branch2's clock. This leads to /inconsistent state snapshots/ because, at time T=12:00, a money transfer is recorded as received at Branch2, whereas it is not recorded as sent at Branch1.
Theory of distributed systems shrugs and doesn't even try. Theory abstracts away from the physical clock and uses logical clocks for ordering events. These are basically counters, as in Lamport's clocks and vector clocks. The causality relationship captured by these logical clocks is defined based on passing of information rather than passing of time. As such, it is not possible to query events in relation to physical time.
Recently, we introduced a third option, hybrid clocks. Hybrid clocks combine the best of logical and physical clocks and avoid their disadvantages. Hybrid clocks are loosely synchronized using NTP, yet they also provide provable comparison conditions as in LC or VC.
Our hybrid clocks come in two flavors: hybrid logical clocks (HLC) and hybrid vector clocks (HVC). HLC satisfy the logical clock comparison condition and find applications in multiversion distributed database systems (such as in CockroachDB) where it enables efficient querying of consistent snapshots for read transactions, and ensures that commits of write transactions do not get delayed despite the uncertainties in NTP clock synchronization. HVC satisfy the vector clock comparison condition: in contrast to HLC that can provide a single consistent snapshot for a given time, HVC provide all consistent snapshots for that given time. HVC find applications in debugging and in causal delivery of messages.
The space requirement of VC is shown to be of size n, the number of nodes in the system, which is prohibitive. HVC reduces the overhead of causality tracking in VC by using the fact that the clocks are reasonably synchronized within epsilon. If j does not hear (directly or transitively) from k within epsilon then hvc.j[k] need not be explicitly maintained. We still infer that hvc.j[k] equals hvc.j[j]-epsilon, thanks to clock sync. So hvc.j only maintains entries for nodes that talked to j within last epsilon and provided a fresh timestamp higher than hvc.j[j]-epsilon. This way HVC can potentially scale the VC benefits to many thousands of processes by still maintaining small HVC at each process.
This differential equation captures the rate of propogation of "redness". Red means the node maintains an entry for a node j. Initially only j is red and all other nodes are green. If a red node communicates a message to a green node which is received within epsilon, that node also becomes red (starts maintaining an entry for j in its hvc). A red node may turn back to being green if it doesn't receive a message that contains fresh information about j in the last epsilon.
Our model and simulations show the HVC size is a sigmoid function with respect to increasing epsilon: it has a slow start but grows exponentially after a critical phase transition. Before the phase transition threshold, HVC maintains couple entries per node, however when a threshold is crossed, a node not only gets entries added to its clock from direct interaction but also indirect transfer from another processes HVC, and this makes the HVC entries blow up. In other words, the redness goes viral after a threshold. We derive this threshold as (1/alpha + delta)* ln((2-√3)*(n-1)), for alpha*delta<1.
Our bounds are tight and we find that the size predicted by our model is almost identical to the results obtained by our simulation results.
Practice of distributed systems employs loosely synchronized clocks, mostly using NTP. Unfortunately, perfect synchronization is unachievable due to messaging with uncertain latency, clock skew, and failures. These sync errors lead to anomalies. For example, a send event at Branch1 may be assigned a timestamp greater than the corresponding receive event at Branch2, because Branch1's clock is slightly ahead of Branch2's clock. This leads to /inconsistent state snapshots/ because, at time T=12:00, a money transfer is recorded as received at Branch2, whereas it is not recorded as sent at Branch1.
Theory of distributed systems shrugs and doesn't even try. Theory abstracts away from the physical clock and uses logical clocks for ordering events. These are basically counters, as in Lamport's clocks and vector clocks. The causality relationship captured by these logical clocks is defined based on passing of information rather than passing of time. As such, it is not possible to query events in relation to physical time.
Recently, we introduced a third option, hybrid clocks. Hybrid clocks combine the best of logical and physical clocks and avoid their disadvantages. Hybrid clocks are loosely synchronized using NTP, yet they also provide provable comparison conditions as in LC or VC.
Our hybrid clocks come in two flavors: hybrid logical clocks (HLC) and hybrid vector clocks (HVC). HLC satisfy the logical clock comparison condition and find applications in multiversion distributed database systems (such as in CockroachDB) where it enables efficient querying of consistent snapshots for read transactions, and ensures that commits of write transactions do not get delayed despite the uncertainties in NTP clock synchronization. HVC satisfy the vector clock comparison condition: in contrast to HLC that can provide a single consistent snapshot for a given time, HVC provide all consistent snapshots for that given time. HVC find applications in debugging and in causal delivery of messages.
The space requirement of VC is shown to be of size n, the number of nodes in the system, which is prohibitive. HVC reduces the overhead of causality tracking in VC by using the fact that the clocks are reasonably synchronized within epsilon. If j does not hear (directly or transitively) from k within epsilon then hvc.j[k] need not be explicitly maintained. We still infer that hvc.j[k] equals hvc.j[j]-epsilon, thanks to clock sync. So hvc.j only maintains entries for nodes that talked to j within last epsilon and provided a fresh timestamp higher than hvc.j[j]-epsilon. This way HVC can potentially scale the VC benefits to many thousands of processes by still maintaining small HVC at each process.
HVC bounds
But how effective are HVC for reducing the size of VC? To address this question, we developed an analytical model that uses four parameters, epsilon: uncertainty of clock synchronization, delta: minimum message delay, alpha: message sending rate, and n: number of nodes in the system. We use a model with random unicast message transmissions and derive the size of HVC in terms of a delay differential equation.This differential equation captures the rate of propogation of "redness". Red means the node maintains an entry for a node j. Initially only j is red and all other nodes are green. If a red node communicates a message to a green node which is received within epsilon, that node also becomes red (starts maintaining an entry for j in its hvc). A red node may turn back to being green if it doesn't receive a message that contains fresh information about j in the last epsilon.
Our model and simulations show the HVC size is a sigmoid function with respect to increasing epsilon: it has a slow start but grows exponentially after a critical phase transition. Before the phase transition threshold, HVC maintains couple entries per node, however when a threshold is crossed, a node not only gets entries added to its clock from direct interaction but also indirect transfer from another processes HVC, and this makes the HVC entries blow up. In other words, the redness goes viral after a threshold. We derive this threshold as (1/alpha + delta)* ln((2-√3)*(n-1)), for alpha*delta<1.
Our bounds are tight and we find that the size predicted by our model is almost identical to the results obtained by our simulation results.



Comments