Designing Access Methods: The RUM Conjecture

This paper is from EDBT 2016. Database veterans would know of the tradeoffs mentioned here, but it is very useful to have this "systematization of knowledge" paper, because it gives a good mental framework for new-comers to the field, and seeing practical/implicit tradeoffs explicitly stated can create an epiphany for even the veterans.

The problem

Algorithms and data structures for organizing and accessing data are called access methods. Database research/development community has been playing catchup redesigning and tuning access methods to accommodate changes to hardware and workload. As data generation and workload diversification grow exponentially, and hardware advances introduce increased complexity, the effort for the redesigning and tuning have been accumulating as well. The paper suggests it is important to solve this problem once and for all by identifying tradeoffs access methods face, and designing access methods that can adapt and autotune the structures and techniques for the new environment.
 
The paper identifies RUM (read/update/memory overhead)  tradeoff as the main tradeoff access methods face, explores how existing data structures explored the tradeoff space, and envisions a future where the RUM Conjecture will create a trend toward building access methods that can efficiently morph to support changing requirements and different software and hardware environments.

The RUM tradeoff

The Read overhead (RO) of an access method (aka read amplification) is the ratio between the total amount of data accessed including auxiliary data (e.g. data read to traverse a B+-tree) and base data, divided by the amount of retrieved base data.

The Update Overhead (UO) (aka write amplification) is given by the amount of updates applied to the auxiliary data in addition to the updates to the main data. For the B+-tree example, the UO is calculated by dividing the updated data size (both base and auxiliary B+-tree node data) by the size of the updated base data.

The Memory Overhead (MO) (aka space amplification) is the space overhead induced by storing auxiliary data. For the B+-tree example, the MO is computed by dividing the overall size of the B+-Tree by the base data size.

The theoretical minimum for each overhead is to have the ratio equal to 1.0, implying that the base data is always read and updated directly and no extra bit of memory is wasted. Achieving these bounds for all three overheads simultaneously, however, is not possible as there is always a price to pay for every optimization.

Hypothesis. An access method that is optimal with respect to one of the read, update, and memory overheads, cannot achieve the optimal value for both remaining overheads.

The RUM Conjecture

The RUM conjecture generalizes the above hypothesis to upperbounding overhead rather than insisting on 0-overhead optimal point. Even with this generalization, it claims there is an impossibility. (Conjecture means not proven. When it is proven using some model definitions/axioms and logic, it becomes a theorem. See the transition of CAP conjecture to CAP theorem.)


The RUM Conjecture: An access method that sets an upper bound for two of the read, update, and memory overheads, incurs a hard lower bound for the third overhead which cannot be further reduced.

RUM in practice

Read optimized access method examples include indexes with constant time access such as hash-based indexes or logarithmic time structures such as B-Trees, Tries, Prefix B-Trees, and Skiplists.

Write optimized access methods consolidate updates and apply them in bulk to the base data. Examples include the Log-structured Merge Tree, the Partitioned B-tree, the Materialized Sort-Merge (MaSM) algorithm, the Stepped Merge algorithm, and the Positional Differential Tree. LA-Tree and FD-Tree are designed to leverage strengths and accommodate weaknesses of flash storage.

Space optimized access methods include compression techniques and lossy index structures such as Bloom filters, lossy hash-based indexes like count-min sketches, bitmaps with lossy encoding, and approximate tree indexing. Sparse indexes, which are light-weight secondary indexes, like ZoneMaps, Small Materialized Aggregates and Column Imprints fall into the same category.

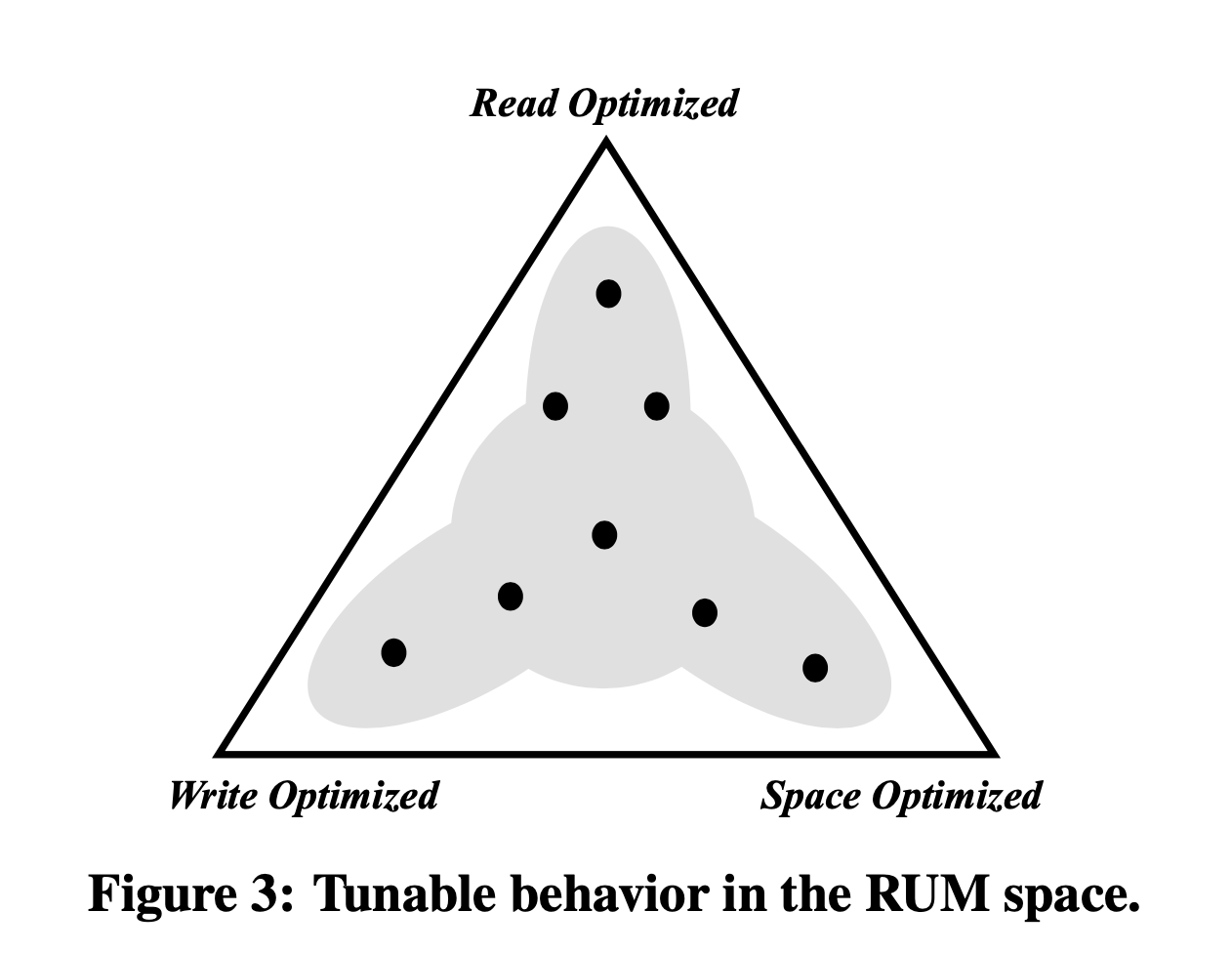
Adaptive access methods (the center of the triangle above) are comprised of flexible data structures designed to gradually balance the RUM tradeoffs by using the workload access pattern as a guide. Most existing data structures provide tunable parameters that can be used to balance the RUM tradeoffs offline, however, adaptive access methods balance the tradeoffs online across a larger area of the design space. Notable proposals are Database Cracking, Adaptive Merging, and Adaptive Indexing, which balance the read performance versus the overhead of creating an index. The incoming queries dictate which part of the index should be fully populated and tuned. The index creation overhead is amortized over a period of time, and it gradually reduces the read overhead, while increasing the update overhead, and slowly increasing the memory overhead.

The paper mentions that real systems have memory/storage hierarchies which make it harder to design and tune access methods. "Data is stored persistently only at the lower levels of the hierarchy and is replicated, in various forms, across all levels of the hierarchy; each memory level experiences different access patterns, resulting in different read and write overheads, while the space overhead at each level depends on how much data is cached." The paper argues that RUM tradeoffs still hold for each level individually and it is possible to reduce overheads at a lower level, by trading off another overhead at a higher level.

Vision

The paper envisions that with tunable behavior access methods, we can solve the constant redesign/re-tuning of access methods for adapting them to new environments (e.g., solid-state drives, multicores, and deep non-uniform memory hierarchies). The ideal RUM access method will be able to seamlessly transition between the three extremes: read optimized, write optimized, and space optimized, as shown in Figure 3. In practice, it may not be feasible to aim for building a single access method able to cover the whole spectrum. Instead, an alternative approach is to build multiple access methods able to navigate partly in the RUM space, however, covering the whole space in aggregate. These may include:

• B+-Trees that have dynamically tuned parameters, including tree height, node size, and split condition, in order to adjust the tree size, the read cost, and the update cost at runtime.
• Approximate (tree) indexing that supports updates with low read performance overhead, by absorbing them in updatable probabilistic data structures (like quotient filters).
• Morphing access methods, combining multiple shapes at once. Adding structure to data gradually with incoming queries, and building supporting index structures when further data reorganization becomes infeasible.
• Update-friendly bitmap indexes, where updates are absorbed using additional, highly compressible, bitvectors which are gradually merged.
• Access methods with iterative logs enhanced by probabilistic data structures that allows for more efficient reads and up- dates by avoiding accessing unnecessary data at the expense of additional space.

Discussion

1/ What about distributed databases?
It is important to remember that RUM conjecture is discussed for a single node database/datastore, and not for a distributed system. For a distributed database, RUM may still apply though. This is an interesting question to think about and discuss.

For distributed systems, other interesting tradeoffs also apply. One of them is PACELC, which says: IF Partition, choose between Availability and Consistency ELSE choose between Latency and Consistency. There are many levels of consistency to tradeoff from (and isolation levels as well). The causal consistency result showed that natural causal consistency, a strengthening of causal consistency that respects the real-time ordering of operations, provides a tight bound on consistency semantics that can be enforced without compromising availability and convergence.



2/ Isn't memory cheap?
I am sure about which two sides of the RUM trilemma I will choose, RU? (See what I did there?) SSDs help a lot to skew the tradeoff domain significantly, but it is still true that memory cost can be an issue so it may not be so clear cut to go for an RU system.

3/ Unified autotuning access methods seem like a good idea, but what would be its drawbacks?
Complexity would be one. Modal behavior, and difficulty of debugging would be an issue. Also would it be able to autotune to exploit the strengths of a given hardware? (Would it need to make measurements and adapt based on that?)

That being said, another advantage of an autotuning access method (if we can pull it off well) can come from fault-tolerance and load-management and maybe even dealing with metastability issues.