SOSP19 Verifying Concurrent, Crash-safe Systems with Perennial
This paper is by Tej Chajed (MIT CSAIL), Joseph Tassarotti (MIT CSAIL), Frans Kaashoek (MIT CSAIL), Nickolai Zeldovich (MIT CSAIL).
Replicated disk systems, such as file systems, databases, and key-value stores, need both concurrency (to provide high performance) and crash safety (to keep your data safety). The replicated disk library is subtle, but the paper shows how to systematically reason about all possible executions using verification. (This work considers verification of a single computer storage system with multiple disk --not a distributed storage system.)
Existing verification frameworks support either concurrency (CertiKOS [OSDI ’16], CSPEC [OSDI ’18], AtomFS [SOSP ’19]) or crash safety (FSCQ [SOSP ’15], Yggdrasil [OSDI ’16], DFSCQ [SOSP ’17]).
Combining verified crash safety and concurrency is challenging because:
Perennial introduces 3 techniques to address these three challenges:
The presentation deferred to the paper for the first two techniques and explained the recovery helping technique.
To show that the implementation satisfies the high-level specification a forward simulation is shown under an abstraction relation. The abstraction relation maps the concrete/implementation state to the high-level abstract specification state. Perennial adopted the abstraction relation as: "if not locked (due to an operation in progress), then the abstract state matches the concrete state in both disks".
The problem is "crashing" breaks the abstraction relation. To fix this problem, Perennial separates crash invariant (which refers to interrupted spec operations) from the abstraction invariant. The recovery proof relies on the crash invariant to restore the abstraction invariant.
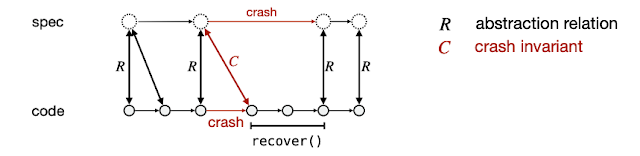
Crash invariant says "if disks disagree, some thread was writing the value on the first disk". Then the recovery helping technique helps recovery commit writes from before the crash. The recovery proof shows the code restores the abstraction relation by completing all interrupted writes. As a result users get correct behavior and atomicity.
The Perennial proof framework was written in 9K lines of coq which provides crash reasoning: leases, memory versioning, and recovery helping. Perennial is built on top of Iris concurrency framework (for concurrency reasoning), which is built on top of Coq. (Iris: R. Krebbers, R. Jung, A. Bizjak, J.-H. Jourdan, D. Dreyer, and L. Birkedal. The essence of higher-order concurrent separation logic. In Proceedings of the 26th European Symposium on Programming Languages and Systems, pages 696–723, Uppsala, Sweden, Apr. 2017.)
The authors have developed Goose for reasoning about Go implementations, but they also defer this to the paper. The developer writes Go code, and the Goose translator (written in 2K lines of Go code) translates this to Perennial proof, where it is machine checked with Coq.

As evaluation of Perennial framework, they verified a mail server written in Go. They argue that compared to a verification in CSCSPEC [OSDI ’18] (their earlier verification framework), the verification in Perennial takes less effort and is done in less number of lines of proof.

The software is available at https://chajed.io/perennial.
1. Is this an instance of a convergence refinement relation?
In 2001, I was thinking on fault-tolerance preserving refinements as a graduate student working on graybox design of self-stabilization. The question was that: If we design fault-tolerance at the abstract, what guarantee do we have that after the abstract code is compiled and implemented in concrete, the fault-tolerance still holds/works?
It is easy to see that fault-tolerance would be preserved by an "everywhere refinement" that preserves the abstraction relation (between concrete and abstract) at any state, including the states outside the invariant states that are not reachable in the absence of faults. But the problem is that outside the invariant, the abstraction relation may not hold due to recovery actions being different than normal actions. That is pretty much the dilemma the Perennial work faced in verifying the recovery of replicated disks above.
OK, I said, let's relax the everywhere refinement to an "everywhere eventual refinement" and that would work for preserving fault-tolerance. Yes, it works, but it is not easy to prove that the concrete is an everywhere eventual refinement of the abstract because there is a lot of freedom in this type of refinement, and not much of a structure to leverage. The proof becomes as hard as proving fault-tolerance of the concrete from scratch. So, what I ended up proposing was a "convergent refinement", where the actions of the concrete provides a compacted version of the actions of the abstract outside the invariant. In other words, the forward simulation outside the invariant would be skipping states in the concrete. Perennial faced with the same dilemma chose to use a different abstraction relation. Whereas the convergence refinement idea is to keep the same abstraction relation but allow it to contract/skip steps in the computations outside the invariant states. I wonder if this could be applicable in the Perennial problem.
My reasoning with going compacting steps in refinement outside invariant was because it is safer than expanding the computation: if you show recovery in states in the abstract, by skipping steps (and not adding new ones) the concrete is also guaranteed to preserve that recovery.
Here is the abstract of my 2002 paper on convergence refinement. I just checked and this paper only got 19 citations in 19 years. It did not age well after getting a best paper award at ICDCS'02. In comparison, some of the papers we wrote quickly and published as short paper or as a workshop paper got more than 150-900 citations in less than 10 years. Citations is funny business.
Replicated disk systems, such as file systems, databases, and key-value stores, need both concurrency (to provide high performance) and crash safety (to keep your data safety). The replicated disk library is subtle, but the paper shows how to systematically reason about all possible executions using verification. (This work considers verification of a single computer storage system with multiple disk --not a distributed storage system.)
Existing verification frameworks support either concurrency (CertiKOS [OSDI ’16], CSPEC [OSDI ’18], AtomFS [SOSP ’19]) or crash safety (FSCQ [SOSP ’15], Yggdrasil [OSDI ’16], DFSCQ [SOSP ’17]).
Combining verified crash safety and concurrency is challenging because:
- Crash and recovery can interrupt a critical section,
- Crash can wipe in-memory state, and
- Recovery logically completes crashed threads' operations.
Perennial introduces 3 techniques to address these three challenges:
- leases to address crash and recovery interrupting a critical section,
- memory versioning to address crash wiping in-memory state, and
- recovery helping to address problems due to interference from recovery actions.
The presentation deferred to the paper for the first two techniques and explained the recovery helping technique.
To show that the implementation satisfies the high-level specification a forward simulation is shown under an abstraction relation. The abstraction relation maps the concrete/implementation state to the high-level abstract specification state. Perennial adopted the abstraction relation as: "if not locked (due to an operation in progress), then the abstract state matches the concrete state in both disks".
The problem is "crashing" breaks the abstraction relation. To fix this problem, Perennial separates crash invariant (which refers to interrupted spec operations) from the abstraction invariant. The recovery proof relies on the crash invariant to restore the abstraction invariant.

Crash invariant says "if disks disagree, some thread was writing the value on the first disk". Then the recovery helping technique helps recovery commit writes from before the crash. The recovery proof shows the code restores the abstraction relation by completing all interrupted writes. As a result users get correct behavior and atomicity.
The Perennial proof framework was written in 9K lines of coq which provides crash reasoning: leases, memory versioning, and recovery helping. Perennial is built on top of Iris concurrency framework (for concurrency reasoning), which is built on top of Coq. (Iris: R. Krebbers, R. Jung, A. Bizjak, J.-H. Jourdan, D. Dreyer, and L. Birkedal. The essence of higher-order concurrent separation logic. In Proceedings of the 26th European Symposium on Programming Languages and Systems, pages 696–723, Uppsala, Sweden, Apr. 2017.)
The authors have developed Goose for reasoning about Go implementations, but they also defer this to the paper. The developer writes Go code, and the Goose translator (written in 2K lines of Go code) translates this to Perennial proof, where it is machine checked with Coq.

As evaluation of Perennial framework, they verified a mail server written in Go. They argue that compared to a verification in CSCSPEC [OSDI ’18] (their earlier verification framework), the verification in Perennial takes less effort and is done in less number of lines of proof.

The software is available at https://chajed.io/perennial.
MAD questions
1. Is this an instance of a convergence refinement relation?
In 2001, I was thinking on fault-tolerance preserving refinements as a graduate student working on graybox design of self-stabilization. The question was that: If we design fault-tolerance at the abstract, what guarantee do we have that after the abstract code is compiled and implemented in concrete, the fault-tolerance still holds/works?
It is easy to see that fault-tolerance would be preserved by an "everywhere refinement" that preserves the abstraction relation (between concrete and abstract) at any state, including the states outside the invariant states that are not reachable in the absence of faults. But the problem is that outside the invariant, the abstraction relation may not hold due to recovery actions being different than normal actions. That is pretty much the dilemma the Perennial work faced in verifying the recovery of replicated disks above.
OK, I said, let's relax the everywhere refinement to an "everywhere eventual refinement" and that would work for preserving fault-tolerance. Yes, it works, but it is not easy to prove that the concrete is an everywhere eventual refinement of the abstract because there is a lot of freedom in this type of refinement, and not much of a structure to leverage. The proof becomes as hard as proving fault-tolerance of the concrete from scratch. So, what I ended up proposing was a "convergent refinement", where the actions of the concrete provides a compacted version of the actions of the abstract outside the invariant. In other words, the forward simulation outside the invariant would be skipping states in the concrete. Perennial faced with the same dilemma chose to use a different abstraction relation. Whereas the convergence refinement idea is to keep the same abstraction relation but allow it to contract/skip steps in the computations outside the invariant states. I wonder if this could be applicable in the Perennial problem.
My reasoning with going compacting steps in refinement outside invariant was because it is safer than expanding the computation: if you show recovery in states in the abstract, by skipping steps (and not adding new ones) the concrete is also guaranteed to preserve that recovery.
Here is the abstract of my 2002 paper on convergence refinement. I just checked and this paper only got 19 citations in 19 years. It did not age well after getting a best paper award at ICDCS'02. In comparison, some of the papers we wrote quickly and published as short paper or as a workshop paper got more than 150-900 citations in less than 10 years. Citations is funny business.
Refinement tools such as compilers do not necessarily preserve fault-tolerance. That is, given a fault-tolerant program in a high-level language as input, the output of a compiler in a lower-level language will not necessarily be fault-tolerant. In this paper, we identify a type of refinement, namely "convergence refinement", that preserves the fault-tolerance property of stabilization. We illustrate the use of convergence refinement by presenting the first formal design of Dijkstra’s little-understood 3-state stabilizing token-ring system. Our designs begin with simple, abstract token-ring systems that are not stabilizing, and then add an abstract "wrapper" to the systems so as to achieve stabilization. The system and the wrapper are then refined to obtain a concrete token-ring system, while preserving stabilization. In fact, the two are refined independently, which demonstrates that convergence refinement is amenable for "graybox" design of stabilizing implementations, i.e., design of system stabilization based solely on system specification and without knowledge of system implementation details.


Comments