Deep Learning With Dynamic Computation Graphs (ICLR 2017)
This is a paper by Google that is under submission to ICLR 2017. Here is the OpenReview link for the paper. The paper pdf as well as paper reviews are openly available there. What a concept!
This paper was of interest to me because I wanted to learn about dynamic computation graphs. Unfortunately almost all machine learning/deep learning (ML/DL) frameworks operate on static computation graphs and can't handle dynamic computation graphs. (Dynet and Chainer are exceptions).
Using dynamic computation graphs allows dealing with recurrent neural networks (RNNs) better, among other use cases. (Here is a great article about RNNs and LSTMs. Another good writeup on RNNs is here.) TensorFlow already supports RNNs, but by adding padding to ensure that all input data are of the same size, i.e., the maximum size in the dataset/domain. Even then this support is good only for linear RNNs not good for treeRNNs which is suitable for more advanced natural language processing.
This was a very tough paper to read. It was definitely above my level as a beginner. The paper assumed a lot of background from the reader. It assumed familiarity with TensorFlow execution and operators, and also some understanding of programming language background and familiarity with RNNs. The dynamic batching idea introduced in the paper is a complex idea but it is explained briefly (and maybe a bit poorly?) in one page. Even when I gave the paper all my attention, and tried to form several hypothesis of dynamic batching idea, I was unable to make progress. At the end, I got help from a friend who is an expert at deep learning.
I skipped reading the second part of the paper which introduced a combinator library for NNs. The library is relevant because it was instrumental in implementing the dynamic batching idea introduced in the first part of the paper. This second part looked interesting but the functional programming language concepts discussed was hard for me to follow.
Batching is important because GPUs crave for batching, especially when dealing with text data where each item is of small size. (While images are already large enough to fill/busy the GPU, but that is not so for text data.)
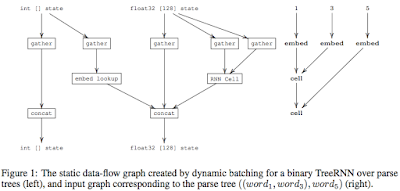
However, the challenge for batching when using DCGs is that the graph of operations is not static, and can be different for every input. The dynamic batching algorithm fixes batching for DCGs. Given a set of computation graphs as input, each of which has a different size and topology, dynamic batching algorithm will rewrite the graphs by batching together all instances of the same operation that occur at the same depth in the graph. (Google is really into graph rewriting.)
The dynamic batching algorithm takes as input a batch of multiple input graphs and treats them as a single disconnected graph. Source nodes are constant tensors, and non-source nodes are operations. Scheduling is performed using a greedy algorithm: (I omit some of the more detailed steps in the paper.)
Dynamic batching instantiates each operation only once, and invokes it once for each depth, so the number of kernel invocations is log(n), rather than n, where n is tree size. Dynamic batching thus achieves substantial speedups even at batch size 1, because it batches operations at the same depth within a single tree.
This Google paper doesn't cite or talk about Dynet and Chainer, but Dynet and Chainer are single machine ML/DL frameworks that support dynamic computation graphs. On one hand, Dynet & Chainer are most likely not good at batching, and the dynamic batching method here has contribution. On the other hand, since Dynet & Chainer support dynamic computation graphs natively (rather than by way of emulating it on static computation graphs like dynamic batching does), they are most likely more expressive than the dynamic batching can achieve. In fact, another limitation of the dynamic batching approach is that it requires all operations that might be used to be specified in advance. Each input/output may have a different type but all types must be fixed and fully specified in advance.
This paper was of interest to me because I wanted to learn about dynamic computation graphs. Unfortunately almost all machine learning/deep learning (ML/DL) frameworks operate on static computation graphs and can't handle dynamic computation graphs. (Dynet and Chainer are exceptions).
Using dynamic computation graphs allows dealing with recurrent neural networks (RNNs) better, among other use cases. (Here is a great article about RNNs and LSTMs. Another good writeup on RNNs is here.) TensorFlow already supports RNNs, but by adding padding to ensure that all input data are of the same size, i.e., the maximum size in the dataset/domain. Even then this support is good only for linear RNNs not good for treeRNNs which is suitable for more advanced natural language processing.
This was a very tough paper to read. It was definitely above my level as a beginner. The paper assumed a lot of background from the reader. It assumed familiarity with TensorFlow execution and operators, and also some understanding of programming language background and familiarity with RNNs. The dynamic batching idea introduced in the paper is a complex idea but it is explained briefly (and maybe a bit poorly?) in one page. Even when I gave the paper all my attention, and tried to form several hypothesis of dynamic batching idea, I was unable to make progress. At the end, I got help from a friend who is an expert at deep learning.
I skipped reading the second part of the paper which introduced a combinator library for NNs. The library is relevant because it was instrumental in implementing the dynamic batching idea introduced in the first part of the paper. This second part looked interesting but the functional programming language concepts discussed was hard for me to follow.
The dynamic batching idea
This paper introduces dynamic batching idea to emulate dynamic computation graphs (DCGs) of arbitrary shapes and sizes over TensorFlow which only supports static computation graphs.Batching is important because GPUs crave for batching, especially when dealing with text data where each item is of small size. (While images are already large enough to fill/busy the GPU, but that is not so for text data.)
However, the challenge for batching when using DCGs is that the graph of operations is not static, and can be different for every input. The dynamic batching algorithm fixes batching for DCGs. Given a set of computation graphs as input, each of which has a different size and topology, dynamic batching algorithm will rewrite the graphs by batching together all instances of the same operation that occur at the same depth in the graph. (Google is really into graph rewriting.)
The dynamic batching algorithm takes as input a batch of multiple input graphs and treats them as a single disconnected graph. Source nodes are constant tensors, and non-source nodes are operations. Scheduling is performed using a greedy algorithm: (I omit some of the more detailed steps in the paper.)
- Assign a depth, d, to each node in the graph. Nodes with no dependencies (constants) are assigned depth zero. Nodes with only dependencies of depth zero, are assigned depth one, and so on.
- Batch together all nodes invoking the same operation at the same depth into a single node.
- Concatenate all outputs which have the same depth and tensor type. The order of concatenation corresponds to the order in which the dynamic batching operations were enumerated.
Experimental results
The test results emphasize the importance of batching, especially on GPUs where it can enable speed ups up to 120x. The speedup ratio denotes the ratio between the per-tree time for dynamic batching on random shapes ("full dynamic"), versus manual batching with a batch size of 1.Dynamic batching instantiates each operation only once, and invokes it once for each depth, so the number of kernel invocations is log(n), rather than n, where n is tree size. Dynamic batching thus achieves substantial speedups even at batch size 1, because it batches operations at the same depth within a single tree.
Limitations
Dynamic batching works on a single machine, it is not distributed. Dynamic batching requires an all to all broadcasts, so it doesn't scale to distributed machines.This Google paper doesn't cite or talk about Dynet and Chainer, but Dynet and Chainer are single machine ML/DL frameworks that support dynamic computation graphs. On one hand, Dynet & Chainer are most likely not good at batching, and the dynamic batching method here has contribution. On the other hand, since Dynet & Chainer support dynamic computation graphs natively (rather than by way of emulating it on static computation graphs like dynamic batching does), they are most likely more expressive than the dynamic batching can achieve. In fact, another limitation of the dynamic batching approach is that it requires all operations that might be used to be specified in advance. Each input/output may have a different type but all types must be fixed and fully specified in advance.
While writing this post, I came across this blog post from June 2016. It looks like this guy came up with the simple version of dynamic batching idea as he was trying to implement treeRNNs in TensorFlow. The implementation there however doesn't include batching.
By clicking on label "mldl" at the end of the post, you can reach all of my posts about machine learning / deep learning (ML/DL).
By clicking on label "mldl" at the end of the post, you can reach all of my posts about machine learning / deep learning (ML/DL).




Comments
any article explains that?