Hybrid Logical Clocks
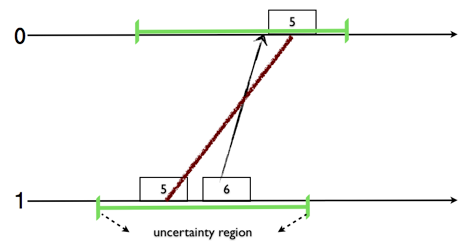
Here I will write about our recent work on Hybrid Logical Clocks, which provides a feasible alternative to Google's TrueTime. A brief history of time (in distributed systems) Logical Clocks (LC) was proposed in 1978 by Lamport for ordering events in an asynchronous distributed system. LC has several drawbacks for modern systems. Firstly, LC is divorced from physical time (PT), as a result we cannot query events in relation to real-time. Secondly, to capture happened-before relations, LC assumes that there are no backchannels and all communication occurs within the system. Physical Time (PT) leverages on physical clocks at nodes that are synchronized using the Network Time Protocol (NTP). PT also has several drawbacks. Firstly, in a geographically distributed system obtaining precise clock synchronization is very hard; there will unavoidably be uncertainty intervals. Secondly, PT has several kinks such as leap seconds and non-monotonic updates. And, when the uncertaint...


