CRDTs: Consistency without concurrency control

This paper appeared in ACM SIGOPS Operating Systems Review in April 2010. One of the authors on this paper is Marc Shapiro. We have previously discussed the "optimistic replication" survey by Shapiro here. (If you haven't read that survey, you should take a moment now to fill this gap. I'll wait.)

This paper is also related to optimistic replication. Recall that there are two approaches to replication due to the CAP theorem. One approach insists on maintaining a strong consistency among replicas and requires consensus for serializing all updates on the replicas. Unfortunately this approach does not scale beyond a small cluster. The alternative, optimistic replication, ensures scalability by giving up consistency guarantees, however in the absence of consistency, application programmers are faced with overwhelming complexity. Yes, for some applications eventual consistency may suffice, but even there "complexity and consensus are hiding under a different guise, namely of conflict detection and resolution".

(In the review below, I re-used sentences--and often whole paragraphs-- from the paper without paraphrasing. Those original sentences expressed the content clearly, and I got lazy. Sorry.)

What this paper shows is in some (limited) cases, a radical simplification is possible. If concurrent updates to some datum commute, and all of its replicas execute all updates in causal order, then the replicas converge. The paper calls these data types whose operations commute when they are concurrent as Commutative Replicated Data Types (CRDTs). The CRDT approach ensures that there are no conflicts, hence, no need for consensus-based concurrency control. Replicas of a CRDT eventually converge without any complex concurrency control. As an existence proof of non-trivial, useful, practical and efficient CRDT, the paper presents one that implements an ordered set with insert-at-position and delete operations. It is called Treedoc, because sequence elements are identified compactly using a naming tree, and because its first use was concurrent document editing. The paper presents some experimental data based on Wikipedia traces.

Now, on with the details of the Treedoc data structure and application.

Model

The paper considers a collection of sites (i.e., networked computers), each carrying a replica of a shared ordered-set object, and connected by a reliable broadcast protocol (e.g., epidemic communication). This approach supports a peer-to-peer, multi-master execution model: some arbitrary site initiates an update and executes it against its local replica; each other site eventually receives the operation and replays it against its own replica. All sites eventually receive and execute all operations; causally-related operations execute in order, but concurrent operations may execute in different orders at different sites.

Two inserts or deletes that refer to different IDs commute. Furthermore, operations are idempotent, i.e., inserting or deleting the same ID any number of times has the same effect as once. To ensure commutativity of concurrent inserts, we only need to ensure that no two IDs are equal across sites. The ID allocation mechanism is described next.

ID allocation mechanism

Atom identifiers must have the following properties: (i) Two replicas of the same atom (in different replicas of the ordered-set) have the same identifier. (ii) No two atoms have the same identifier. (iii) An atom's identifier remains constant for the entire lifetime of the ordered-set.2 (iv) There is a total order "<" over identifiers, which defines the ordering of the atoms in the ordered-set. (v) The identifier space is dense. Property (v) means that between any two identifiers P and F, P <>

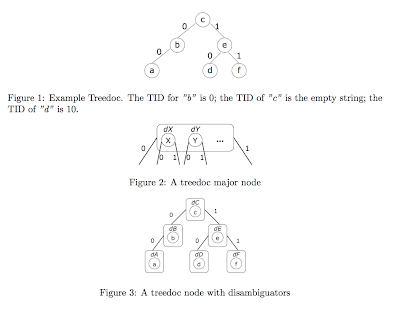
This ID allocation is not difficult at all. The below figures show how it is done.

Treedoc insert and delete

A delete(TID) simply discards the atom associated with TID. The corresponding tree node is retained and marked as a tombstone.

To insert an atom, the initiator site chooses a fresh TID that positions it as desired relative to the other atoms. For instance, to insert an atom R to the right of atom L: If L does not have a right child, the TID of R is the TID of L concatenated with 1 (R becomes the right child of L). Otherwise, if L has a right child Q, then allocate the TID of the leftmost position of the subtree rooted at Q.

Restructuring the tree

Depending on the pattern of inserts and deletes, the tree may become badly unbalanced or riddled with tombstones. To alleviate this problem, a restructuring operation "flatten" transforms a tree into a flat array, eliminating all storage overhead.

However, flattening does not genuinely commute with update operations. This is solved by using an update-wins approach: if a flatten occurs concurrently with an update, the update wins, and the flatten aborts with no effect. A two-phase commit protocol is used for this purpose (or, better, a fault-tolerant variant such as Paxos Commit). The site that initiates the flatten acts as the coordinator and collects the votes of all other sites. Any site that detects an update concurrent to the flatten votes no, otherwise it votes yes. The coordinator aborts the flatten if any site voted no or if some site is crashed.

This commit-based solution also has problems. Commitment protocols are problematic in large-scale and dynamic systems; to alleviate this issue only a small number of (core) servers involve in the flatten, the remaining servers (nebula) copy from these core servers and catch up. This is again another patch, and suffers from other problems (such as converting between flattened and unflattened atom ids during catch-up). The paper explains how to solve those other problems. It is unclear if the catching up leads to availability problems. In any case, it is clear that flattening operation is the less-elegant side of the Treedoc CRDT.

Experiments on Wikipedia edit history

The paper presents experimental results from real-world cooperative editing traces from Wikipedia. A number of Wikipedia pages were stored as Treedocs, interpreting differences between successive versions of a page as a series of inserts and deletes. In some experiments the atoms were words; in the ones reported below an atom is a whole paragraph.

Those sudden drops in the graph are due to the flatten operation.

Discussion

One of the features of Treedoc is that it ensures causal ordering without vector clocks. This is made possible by using an application specific technique: When the replica sees that the node it is inserting does not have a parent inserted on the tree yet, it makes that node wait. In general, though, we would need vector clocks, or logical clocks at least. The paper has this to say on that: "Duplicate messages are inefficient but cause no harm, since operations are idempotent. Therefore, a precise vector clock is not necessary; approximate variants that are scalable may be sufficient as long as they suppress a good proportion of duplicates."

I think this paper opens a very interesting path in the replication jungle. The CRDT technique does not have broad/general applicability. But for the cases where the technique is applicable, the benefit is huge. I wonder if using the Treedoc structure can achieve scalability benefits for collaborative real-time editors (GoogleDocs, Google Wave, EtherPad, SubEthaEdit [a peer-to-peer collaborative editor]).

I have seen a similar idea to CRDT before, in DISC 2001, "Stabilizing Replicated Search Trees". There the idea was to maintain a 2-3 search tree data structure at each replica, and despite transient state corruption (e.g., despite initially starting at different arbitrary states), the replicas eventually converge to the same correct state. In that work however, synchronous replication was required: all update operations were to be executed in the same order at all sites to keep consistency among the replicas. That is a pretty harsh requirement, and a deal breaker for wide area replication.