Streamlet: textbook streamlined blockchains

In this 2020 technical report, the authors claim to present a very simple BFT

consensus protocol. I am taking it that "textbook" in the title is used as praise for simplicity of the algorithm. 

Nakamoto consensus is definitely simpler than Streamlet, but in contrast to Nakamoto consensus Streamlet provides deterministic finalization and does not suffer from the costly proof-of-work (POW) and the low-throughput POW induces. And, among the protocols that provide deterministic finalization, including PBFT, Tendermint, HotStuff, yes, Streamlet is the simplest protocol. So, yes, Streamlet deserves your attention.

Streamlet protocol

Streamlet is an amalgamation of existing techniques. It borrows stuff from Casper, HotStuff, and Elaine Shi's earlier work. But that's OK. The goal is to show the simplest protocol, not necessarily the most novel or the most efficient protocol. Here is the protocol, verbatim from the introduction of the paper.

In Streamlet, each epoch has a designated leader chosen at random by a publicly known hash function. We assume that a valid blockchain is a sequence of blocks cryptographically “chained” together by a hash function, i.e., each block contains a hash of its prefix.

Propose-Vote. In every epoch: 

• The epoch’s designated leader proposes a new block extending from the longest notarized chain it has seen (if there are multiple, break ties arbitrarily). The notion “notarized” is defined below.
• Every player votes for the first proposal they see from the epoch’s leader, as long as the proposed block extends from (one of) the longest notarized chain(s) that the voter has seen. A vote is a signature on the proposed block. 
• When a block gains votes from at least 2n/3 distinct players, it becomes notarized. A chain is notarized if its constituent blocks are all notarized.

Finalize. Notarized does not mean final. If in any notarized chain, there are three adjacent blocks with consecutive epoch numbers, the prefix of the chain up to the second of the three blocks is considered final. When a block becomes final, all of its prefix must be final too.

Is this a simple protocol?

It is a short single action protocol. It looks simple. Let's delve in.

Normal operation is simple, sure. Let's assume synchronous epochs of say 1 second length. If it is node j's turn to propose in this epoch (i.e., at this second) according to the rotation function, j identifies the longest notarized chain, adds the proposed block to that and broadcasts it. The honest nodes vote for j's proposal and broadcast their votes to every node. These are all received within the epoch duration. And that is it. Rinse, repeat. 

Yes, there is all-to-all communication in the vote phase, and that has some cost associated with it. But that also serves to strengthen the resilience of the protocol and makes it easy to rotate the leaders. Since every node gets all the votes, the leader does not need to conclude/teach/finalize anything to the other nodes; each node can do that itself.

Another thing that helps with resilience is that Streamlet performs consensus on chains rather than individual consensus instances. The big idea in Streamlet is that the chain matters and should be leveraged. Unlike PBFT and its derivatives, which treats each consensus instance isolated and independent of each other, Streamlet leverages the chain structure that links consensus instances to each other. Here consensus on one block is also vote for the previous blocks in the chain. That means even though a block does not get notarized, say because of leader failure before reaching enough nodes, that block can later be grandparented in to finalization when a chain including it gets notarized with three consecutive blocks at its end.

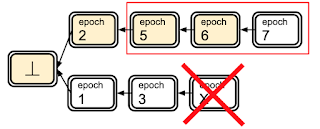
OK, let's now check how the protocol behaves in a partially asynchronous system, where the synchronization assumptions can be violated temporarily. In Figure 1, we see that forks can develop in the absence of synchrony, but according to the finality rule the prefix of the top chain up to the epoch-6 block is considered final. If we had synchrony it wouldn't be possible to have forks, because if 2/3 of the nodes authorize epoch 1 block, they would not be OK with authorizing epoch 2 block linking to the origin block after that. But without the synchrony assumptions, it is possible for both blocks to be proposed without notarization at first and then make progress toward notarization concurrently. That means, epoch 1 block was not notarized when epoch 2 block was added. The leader of 2 did not see 1 notarized (or it could also be that the leader of 2 was Byzantine and ignored it). The notarizations reached to the nodes about 1 and 2 later on. And the same thing happened with epoch 3 and 5 blocks. Even if we required that the nodes vote to epochs in increasing order, and refuse to vote for a lower epoch number block after voting for a higher epoch numbered block this scenario would still be possible. Distributed systems is hard, let's go train neural networks.

The paper includes a proof of why after 5,6,7 is notarized it is impossible to have the other fork to survive. It is an easy to follow proof... again relative to the distributed systems standards.

I really like that the normal action is also the one that works in the asynchronous case. There is no separate detect-and-switch-to-recovery mode when synchrony assumptions are violated. The protocol is self-stabilizing with the normal case action and is always safe to the face of asynchrony.

One thing still lingered in my mind though. I was still super suspicious how there was no need for using the epoch number knowledge in the protocol or the proof. The protocol uses the longest chain rule. Longest chain does not necessarily mean the chain with the highest epoch. It is about how many blocks there are in the chain. As far as the epoch numbers is concerned, the only thing the protocol cares about is to see three consecutive epoch blocks for finalization. The protocol doesn't say about monotonically increasing requirement for epoch numbers in an asynchronous environment (again except for the finality rule which requires 3 consecutive epoch blocks).

So to test that safety is still satisfied with this protocol in an asynchronous setup I modeled Streamlet in TLA+. To be specific, I modeled the crash fault-tolerant version given in the Appendix. But that is actually almost the same as the BFT protocol. It tolerates upto a minority number of nodes crash failing, and the only change is that notarization require only majority votes. The finality rule is still the same. That is another neat thing about Streamlet, almost the same protocol works for byzantine and crash fault-tolerance.

So, what did I find when I modeled Streamlet in TLA+? Was it easy to model it in TLA+? Was there a safety violation in an asynchronous system if we don't require the nodes to be epoch-monotonic in their voting? You will have to wait for the next blog post to hear the answers.

In the meanwhile, I have more questions for you.

MAD questions

1. How can we add pipelining to Streamlet?

If we can add pipelining to Streamlet, that will help improve throughput. Each epoch has the same communication structure, and that is promising for adding pipelining to Streamlet. The question is how do we do that.

2. Is there a vulnerability if the leader is known beforehand?

The epoch leader is known in advance in Streamlet. So a strong network adversary can use this information to block communication from the epoch leader. There are some protocols that hide this information to avoid this vulnerability. I am guessing it may be possible to design the rotating function to hide this information and reveal the leader only at the corresponding epoch, but I am not a cryptologist.

3. Is it easy to get 5 consecutive blocks notarized with Byzantine nodes?

The paper says that in order to make progress, there needs to be 5 consecutive honest leaders after GST. But if 1/3rd of the nodes are Byzantine, and the rotation function is random, it will be a while before we get a sequence of 5 consecutive honest leaders, right? I wonder if this causes any problems.